Rechts- un Linksseitiger Grenzwert an den Polstellen

Question

bei der Funktion (2x³-4x²-10x+12)/(x²+x-6) soll der rechts- und linksseitige Grenzwert an den Polstellen (2 und -3 berechnet werden). 
Bisher habe ich das immer so gemacht, dass ich x mit x₀+h bzw. x₀-h ersetzt, dann ausmultipliziert und gekürzt habe. Bei höheren Potenzen im Nenner wie in diesem Fall wird das allerdings sehr aufwendig. Gibt es da eine schneller Möglichkeit? Muss ich den Zähler überhaupt genauer betrachten, da h sowieso immer gegen 0 läuft? Ich hoffe ihr könnt mir weiterhelfen! Danke und Gruß, Patrick

Answer 1

Du brauchst eigentlich nur im Zähler die Stelle einzusetzen.

Etwa bei x=2 gibt das -8 und im Nenner hast du ja  (x-2)*(x+3)

also bei 2+h ist der Nenner von der Art  - * + also negativ.

und der Zähler auch negativ.

Und Nenner negativ und Zähler auch, also für h gegen 0

ist der GW  + unendlich.

entsprechend bei  2-h ist es  - unendlich.

Comments

Danke für die schnelle Antwort!Also das heißt dass ich im Zähler direkt die Postelle für x einsetzen kann, und nur im Nenner x₀+h für x einsetzen muss?Warum ist der Nenner bei 2+h negativ? Ich hab dann dort stehen: ((2+h)-2)*((2+h)+3)  und ausmultipliziert h²+5h

---

Oh ja, da hatte ich mich vertan.

---

Hallo mathef,

Etwa bei x=2 gibt das -8

ich habe 32 heraus.

mfg Georg

---

Danke, hat sich ja jetzt wohl erledigt.

Answer 2

Du hast vermutlich ja eh schon eine Faktorzerlegung von Zähler und Nenner gemacht

(2·x^3 - 4·x^2 - 10·x + 12) / (x^2 + x - 6)

= (2·(x - 1)·(x + 2)·(x - 3)) / ((x - 2)·(x + 3))

Wir schreiben die Bereiche mal auf die wir haben

_____ |-3| _____ |-2| _____ |+1| _____ |+2| _____ |+3| _____

Was passiert ganz rechts wo das x unendlich groß wird. Da ist Zähler und Nenner positiv und wir haben ein Positives Ergebnis

_____ |-3| _____ |-2| _____ |+1| _____ |+2| _____ |+3| __+__

Da wir alles einfache Nullstellen mit Vorzeichenwechsel haben, ändert sich das Vorzeichen in allen Bereichen

__-__ |-3| __+__ |-2| __-__ |+1| __+__ |+2| __-__ |+3| __+__

Ich färbe mal die Polstellen in einer anderen Farbe

__-__ |-3| __+__ |-2| __-__ |+1| __+__ |+2| __-__ |+3| __+__

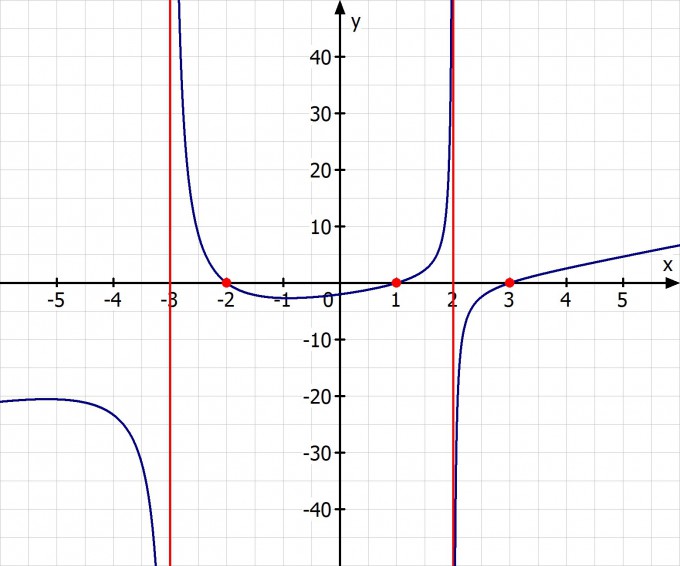
An der Polstelle -3 haben wir also einen Übergang von -unendlich auf +unendlich. An der Polstelle +2 einen Übergang von +unendlich auf -unendlich.

Ich skizziere das mal einschließlich der Nullstellen.

Comments

Mathecoach, ich habe etwas anderes heraus.
Siehe auch den Graph.

mfg Georg

---

Wenn du nächstes mal die Funktion richtig abschreibst, bekommst du dann sicher auch das gleiche heraus wie ich. In der Funktion steht -10x und nicht + 10x.

 ~plot~(2x^3-4x^2-10x+12)/(x^2+x-6) ; [[ -10 | 10 | -100 | 100 ]]~plot~

---

Korrektur,

wie dem mathecoach aufgefallen muß es " -10x und nicht + 10x." heißen.

Es ergeben sich dann die Grenzwerte

Answer 3

In der Frage / Erklärungen sieht es eigentlich so aus als wolltest du
die 1.Ableitung bilden ?

Hier meine Berechungen

Und der Graph

Bin bei Bedarf gern weiter behilflich.

Comments

Korrektur,

wie dem mathecoach aufgefallen muß es " -10x und nicht + 10x." heißen.

Es ergeben sich dann die Grenzwerte

 ~plot~(2x^3-4x^2-10x+12)/(x^2+x-6) ; [[ -10 | 10 | -100 | 100 ]]~plot~