gegenen ist die funktion f mit f(x)=x^2/8(6-x)

Question

Hallo liebe Mathelounge,
ich schreibe die Tage eine Klassenarbeit. Unser Lehrere nimmt häufig Aufgaben dran, die wir zu Hause oder im Unterricht bearbeitet haben.
Diese Aufgabe hatte ich damals als Hausaufgabe auf.

Mir fällt es hierbei leichter dieser nachzuverstehen, wenn diese vorgerechnet wird.
Ich wäre sehr dankbar, wenn jemand sich dafür zeitnehmen könnte und ggf begründen könnte, wie er in dem Fall vorgeht bzw. beim rechnen vorgeht.

Die Punkte O(0|0), A(u|0) und B(u|(f(u)) mit 0< u < 6 sind die Eckpunkte eines Dreiecks.

Answer 1

f(x) = x²/8 • (6-x)

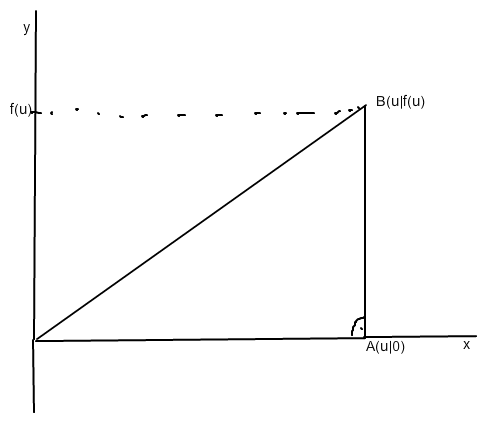
Flächeninhalt  A(u)  =  1/2 • Grundlinie • Höhe = 1/2 • u • f(u) = 1/2 • u • u²/8 • (6-u) = u³ · (6 - u) / 16

A(u)  =  u³ · (6 - u) / 16

u³ · (6 - u) / 16 = 5 

⇔ 3/8 • u³ - 1/16 • u⁴ - 5 = 0

diese Gleichung kann man nur aufwändig explizit nach x auflösen:

Man benutzt ein numerisches Näherungsverfahren, zum Beispiel das

Newtonverfahren:

Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben, findet man immer bessere Werte mit der Formel

x_neu =  x_alt - f(x_alt) / f ' (x_alt)

Infos dazu findest du hier:

https://de.wikipedia.org/wiki/Newton-Verfahren[

[ Lösungen: u  5.526  oder  u = 2.981

Einsetzen in A(u) ergibt jeweils den Flächeninhalt  5 ]

Maximaler Flächeninhalt:

A'(u) = u²· (9 - 2·u) / 8 = 0 

 ⇔ u=0 (trivial)  oder  u = 9/2 (Maximalstelle wegen VZW +→ -)

u=9/2 in A(u) einsetzen ergibt       A_max ≈ 8,543

Gruß Wolfgang