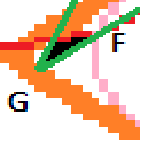Sehr geehrte Damen und Herren, ich bin verzweifelt auf der Suche nach einer Lösung dieser komplizierten Berechnung einer Fläche, welche sich in einem regelmäßigen 5-Eck befindet. Ich habe die Angaben so gut als möglich versucht wiederzugeben und um ein paar Skizzen ergänzt, ich hoffe dass diese verständlich sind. Ich wäre zu größten Dank verpflichtet, wenn man mir mit dieser Berechnung helfen könnte.
Zeichnet man in ein regelmäßiges 5-Eck mit der Seitenlänge (a = 25km) alle Diagonalen ein erhält man u.a. das orange Dreieck ABC, wie in Bild 1 eingezeichnet. Nun wird gezeichnet: in das Dreieck ABC der Innkreis und der Umkreis des kleinen 5-Ecks, welches sich durch die 5 Diagonalen des großen 5-Ecks ergeben hat. (Bild 2). Die beiden Kreise haben nun 2 Schnittpunkte im Dreieck ABC. (E u. F.).
Nun werden noch 2 Geraden (u und v) gezeichnet.
Die Gerade 'u' von Punkt E bis zur Seitenlänge AB des orangen Dreiecks, und zwar so, dass diese auch Punkt F schneidet.Dort wo die gerade 'u' auf die Seitenlänge AB trifft erhalte ich nun Punkt G (Bild 4). Die Gerade 'v' wird nun noch von Punkt 'G' nach Punkt 'H' (Punkt H siehe Bild 1 = Eckpunkt des kleinen 5-Ecks) gezeichnet.
Es geht nun um die Flächenberechnung des schwarz angemalenen Segments des letzten Bildes.
Die grüne Geraden sind die Geraden: u, v / Die Rote Kreisbogen: der Teil des Umkreises des inneren 5-Ecks.
Bild 1: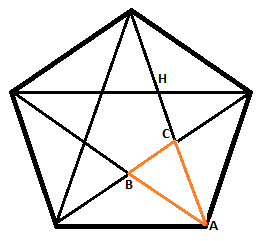 Bild 2:
Bild 2: 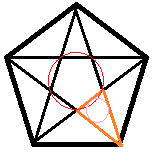 Bild 3 :
Bild 3 :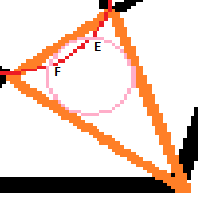 Bild 4:
Bild 4: 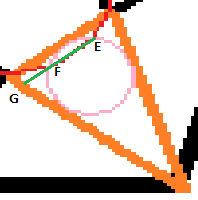
Bild 5: