Gleichung mit drei Punkten aufstellen (LGS drei Unbekannte)

Question

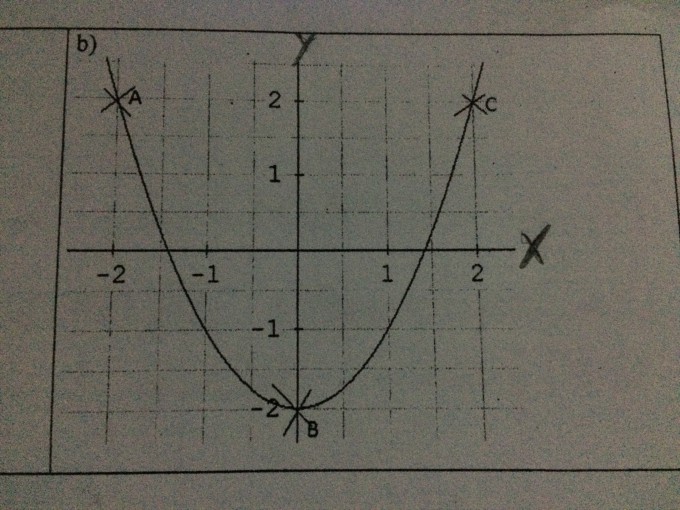
Die Aufgabe wäre eine Gleichung anhand der drei Punkte aufzustellen, indem Lineare Gleichungssysteme mit drei Unbekannten genutzt und berechnet werden.
Hilfsgegenstand um Einsetzverfahren zu umgehen: Casio CG20 Grafiktaschenrechner

Gleichungsformel: a*x^2+b*x+c=y

Mein Rechenweg:
A(-2|2) B(0|-2) C(2|2)

Punkt A: f(-2) = a*( -2 )^2 + b*(-2) + c=2
                                           -4a - 2b + c = 2

Punkt B: f(x) = a* 0^2 + b*0 + c= -2
                              0      +     0 + c= -2

Punkt c: f(2) = a* 2^2 + b*2 + c= 2
                                   4a + 2b + c=2

Eingabe in die Matrix des Taschenrechners unter [A] [F1] [F2]:
( -4  -2  1  [2]          X=?
(  0   0  1 [-2]         Y=?
(  4   2  1 [2]          Z=?

Taschenrechner zeigt an "Keine Lösung" (Fehler)!
Ich bedanke mich schonmal im voraus für das finden des Fehlers!

Answer 1

In der ersten Reihe

( -4  -2  1  [2]          X=?

muß es

( 4  -2  1  [2]          X=?

lauten.

Comments

Eine Vorgehensweise über den Graphen ( da schon einmal vorhanden )
Allgemein :
f ( x ) = a * x^2 + b * x + c
Der Fachmann sieht der Parabel an :
Es ist keine nach links oder rechts verschobene Parabel : b * x entfällt
f ( x ) = a * x^2 + c

Für x = 0 gilt
f ( 0 ) = a * 0^2 + c = -2  => c = -2

f ( x ) = a * x^2 - 2
jetzt noch einen Punkt einsetzen
f  ( 2 ) = a * 2^2 -2 = 2
a * 4 - 2 = 2
a = 1

f ( x ) = x^2 - 2

Answer 2

Punkt A: f(-2) = a*( -2 )² + b*(-2) + c=2
                                           -4a - 2b + c = 2

Hier liegt der Fehler

(-2)^2 = 4 also       +4a - 2b + c = 2

Answer 3

Alternativ für solche Dinge auch gleich die Scheitelpunktform lernen

Öffnungsfaktor

a = (Cy - By) / (Cx - Bx)^2 = (2 - (-2)) / (2 - 0)^2 = 4 / 4 = 1

Scheitelpunktform

f(x) = a * (x - Bx)^2 + By = 1 * (x - 0)^2 + (-2) = x^2 - 2

Dieser Weg wäre wenn nicht gefordert ist das mit einem Gleichungssystem zu machen deutlich einfacher und deutlich schneller. Weiterhin könnte das zur Probe alternativ auf diese Weise gerechnet werden.