Absorptionsgesetz für Photonen. Zerfallsgesetz.

Question

Ich brauche Hilfe bei dieser Aufgabe. Das einzige was ich weiß ist, dass N0 der Startwert ist. ._.

Answer 1

a)

N(x) = N₀ • e^-μx   →  N'(x) = - μ • N₀ • e^-μx

N'(x) = - μ • N(x)  ist die gegebene DGL.

- μ • N₀ • e^-μx  = - μ • N₀ • e^-μx ist wahr,  also ist   N(x) = N₀ • e^-μx  eine Lösung der DGL

b)

Vom Wert f(0) = N₀ fällt N(x) streng monoton. Wegen e^-μx > 0 für alle x ist N(x) ≠ 0 f.a. x

c)

0,9 • N₀ = N₀ • e^-3μ  ↔  e^-3μ = 0,9 ↔  -3μ = ln(0,9)  →   μ = - ln(0,9) / 3 ≈ 0,03512

also:   N(x) = N₀ • e^{- 0,03512·x} 

0,5 • N₀ =  N₀ • e^{- 0,03512·x}   ..... →  x = - ln(0,5) / 0,03512 ≈ 19,4  [ cm ]

d)

N₀ / e =   N₀ • e^{- 0,03512·x}   ↔  e^-1 =  e^{- 0,03512·x}  →  x = 1/ 0,03512 = 28,5 [ cm ]

N₀ / e = 1/e • N₀ ≈ 0,368 N₀ , also 36,8 % der Anfangsintensität

------------

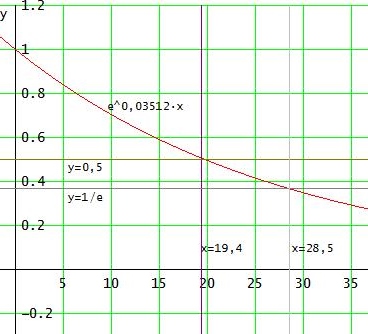
Im folgenden Schaubild ist N₀ = 1, alle Funktionswerte sind also mit N₀ zu multiplizieren:

Gruß Wolfgang