Hallo ich habe hier eine Aufgabe zum Mittelwertsatz der Differentialrechnung ;
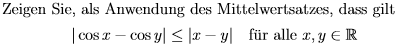
Ich kenne den Mws :
Sei f : [a,b] --> ℝ eine Funktion die auf [a,b] mit a<b definiert und stetig und auch differenzierbar auf (a,b) , dann
existiert ein xo∈(a,b) sodass gilt f´(x0)= (f(b)-f(a))/(b-a).
Es gilt auch das |cos(x)|≤1 für alle x∈ℝ.
was mich verwirrt ist : Was ist den meine Abbildungsvorschrift hier x--> auf |cos(x)|? und wenn ja wie leite ich das denn bitte ab?
Kann mir wer helfen bitte? :)