Gewinn = q1 * (p1 - 1) + q2 * (p2 - 1)
Die Funktionen für q1 und q2 könnte ich hier einsetzen
Gewinn = (-11 - 9p1 + 33p2) * (p1 - 1) + (96 - 52p1 - 16p2) * (p2 - 1)
Ich multipliziere das mal aus
Gewinn = (- 9·p1^2 + 33·p1·p2 - 2·p1 - 33·p2 + 11) + (- 52·p1·p2 + 52·p1 - 16·(p2)^2 + 112·p2 - 96)
Gewinn = - 9·p1^2 - 19·p1·p2 + 50·p1 - 16·p2^2 + 79·p2 - 85
Wir haben maximalen Gewinn wenn die partiellen Ableitungen Null werden
Gewinn/dp1 = - 18·p1 - 19·p2 + 50 = 0
Gewinn/dp2 = - 19·p1 - 32·p2 + 79 = 0
Das LGS hat die Lösung
p1 = 99/215 ∧ p2 = 472/215
p1 = 0.4604651162 ∧ p2 = 2.195348837
Gewinn = 13.22790697
Ich probiere mal eine Skizze zu machen:
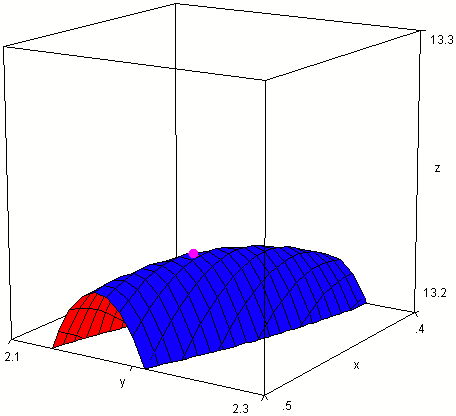
Ich spare mir mal das Ausrechnen der Verkaufsmenge, weil das ja nur noch ein pures Einsetzen ist.
Versuch das ganze mal nachvollziehen. Und eventuell auch die hinreichende Bedingung zu machen, dass dies wirklich ein Maximum ist.