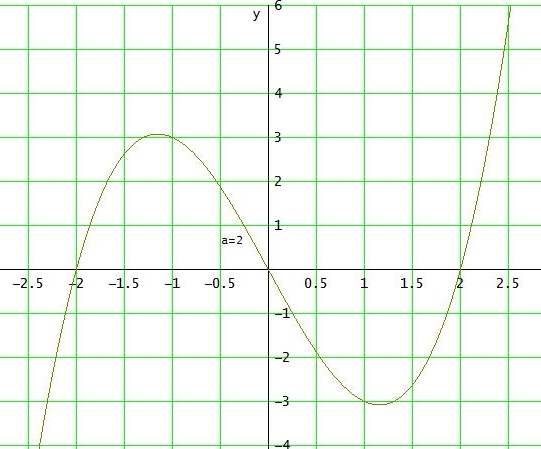
Da die Funktion für jedes a∈ℝ+ symmetrisch zum Ursprung ist (nur ungerade Exponenten von x), stimmen die beiden Flächen für jedes a überein.
Da der Graph für positive x unterhalb der x-Achse verläuft, wird für die rechte Fläche das Integral gleich dem negativen Flächeninhalt :
Ich erhalte 0∫a f(x) dx = a4/4 - 2·a2 = - 4
⇔ a4 - 8a2 + 16 = 0 ⇔ (a2 - 4)2 = 0 ⇔ a2 - 4 = 0 ⇔ a2 = 4
→ a = ± 2 ( -2 entfällt, da a> 0 ) , also a = 2