Integralrechnung mit Flächeninhalt

Question

Ich komme bei 5.2.2 absolut nicht weiter.

Comments

für die Berechnung brauchst du die Nullstellen von f, die man nur aufwändig finden kann:

x = 3.214807191  ∨  x = 12.64610030  ∨  x = -0.8609074992  (Rechnerlösung)

Kennst du ein numerischen Näherungsverfahren (z.B. Newtonverfahren) oder die Cardanischen Formeln?

Oder dürft ihr Gleichungen einfach mit dem TR lösen?

---

Wir kamst du genau auf die Nullstellen, also ich kann das in den Taschenrechner eingeben? aber wie...

und ich kenne leider keins dieser Verfahren.

---

ich habe mir gerade Ihre Zeichnung und so angesehen, nur verstehe ich nicht wie sie auf das u kommen.

Answer 1

5.2.2

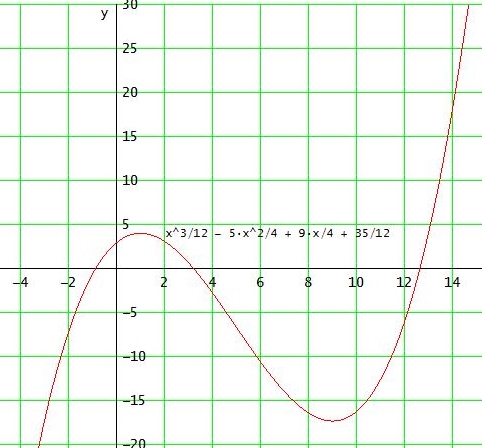
A = ₀∫^u  ( 1/12·x³ - 5/4·x² + 9/4·x + 35/12 ) dx  =  [ x⁴/48 - 5·x³/12 + 9·x²/8 + 35·x/12 ]₀^u

=  u⁴/48 - 5·u³/12 + 9·u²/8 + 35·u/12 = 22/3

Die Gleichung hat die Lösungen

u = 4.301069644  ∨  u = 16.22151013  ∨  u = -2.522579782  ∨  u = 2

Im 1. Quadranten ist nur u = 2  kleiner als die erste Nullstelle  x = 3.21480719

 [ vgl. meinen Kommentar], also ist u = 2 die gesuchte Lösung 

Gruß Wolfgang