Hallo Mariealma,
a)
offensichtlich erwische ich bei dir immer Aufgaben mit falschen Angaben oder lästiger Lösung :-)
f(x) = - 0,18·x3 + 0,85·x2 + 0,6·x + 36,6 = 37
⇔ - 0,18·x3 + 0,85·x2 + 0,6·x - 0,4 = 0
Du willst also die Nullstellen von h(x) = - 0,18·x3 + 0,85·x2 + 0,6·x - 0,4 berechnen.
diese Gleichung kann man nur aufwändig explizit nach x auflösen:
https://de.wikipedia.org/wiki/Cardanische_Formeln
Man benutzt deshalb meist ein numerisches Näherungsverfahren, zum Beispiel das
Newtonverfahren:
Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben, findet man immer bessere Werte mit der Formel:
xneu = xalt - h(xalt) / h ' (xalt) #
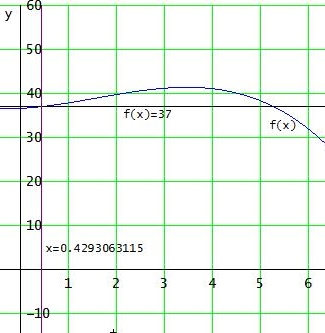
In deinem Fall kannst du den Startwert xalt = 0,4 der Zeichnung entnehmen. Dann musst du h'(x) berechnen und xalt = 0,4 in # einsetzen. Den errechneten Wert für xneu setzt du für xalt noch einmal in # ein usw.
Du hörst auf, wenn sich der neue Wert vom alten bei der von dir gewünschten Stellenzahl nicht mehr unterscheidet.
Mein Rechner gibt die Lösungen
x = -0.9814152809 ∨ x = 0.4293063115 ∨ x = 5.274331191 an.
Nur x = 0.4293063115 liegt in deinem Definitionsbereich 0≤ x ≤ 5. Dieser Lösung solltest du mit dem Startwert x = 0,4 immer näherkommen.
I------
infos dazu findest du auch hier:
https://de.wikipedia.org/wiki/Newton-Verfahren
Gruß Wolfgang