Das ist ein Beispiel aus dem Buch Technische Mechanik 3 von Gross Hauger Schröder Wall.
Beschreibung: Ein Schiff S fährt mit einer konstanten Geschwindigkeit v so, dass der Kurswinkel α gegenüber der Verbindungslinie zum Leuchturm L konstant bleibt. Wie groß ist die Beschleunigung und auf welcher Bahn fährt das Schiff.
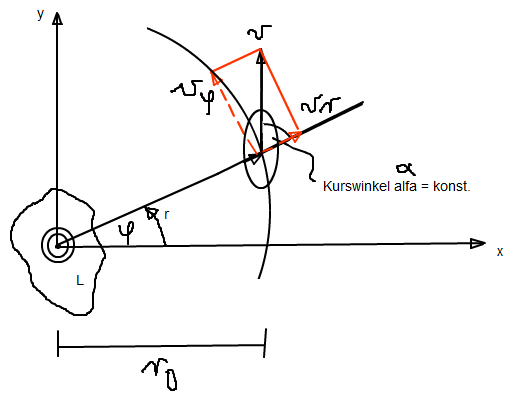
Geschwindigkeitskomponenten sind:
$$ v_r = v \,\cdot \, cos\, \alpha \,\,\,\, radialer \, Richtung$$
$$ v_\phi = v \,\cdot \, sin\, \alpha \,\,\,\, zirkulare \, Richtung $$
radiale Geschw. Komponenten in Polarkoordinaten gilt:
$$v_r = \dot{r} = v \,\cdot \, cos\, \alpha$$
zirkulare Geschw. Komponenten in Polarkoordinaten gilt:
$$ r \cdot \dot{\phi} = v_\phi = v \,\cdot \, sin\, \alpha \,\, \rightarrow \dot{\phi} = \frac{v \,\cdot \, sin\, \alpha}{r} $$
Die Beschleunigung ergibt sich ja durch die Ableitung, dh. $$\ddot{r} =$$ Beschleunigung in radialer Richtung, diese soll $$\ddot{r} =0$$ ergeben. Warum?
die Beschleunigung in zirkularer Richtung ist $$\dot{\phi} $$ abgeleitet.
Wieso ist diese Ableitung ungleich null?
Lösung für die Beschleunigung ist:
$$\ddot{\phi} = \frac{d\dot{\phi}}{dr}\dot{r} = -\frac{v \, sin \, \alpha}{r^2} \cdot\,v \,cos \alpha = - \frac{v^2sin\alpha\,cos\alpha}{r^2}$$
Danke schonmal und sorry für das Zutexten