Bei einem quadratischen Tisch mit der Seitenlänge 1m kann an jeder Seite eine kreisteilförmige Platte ausgeklappt werden, sodass der Tisch kreisförmig wird.
a) Fertige eine Skizze der Tischplatte an.
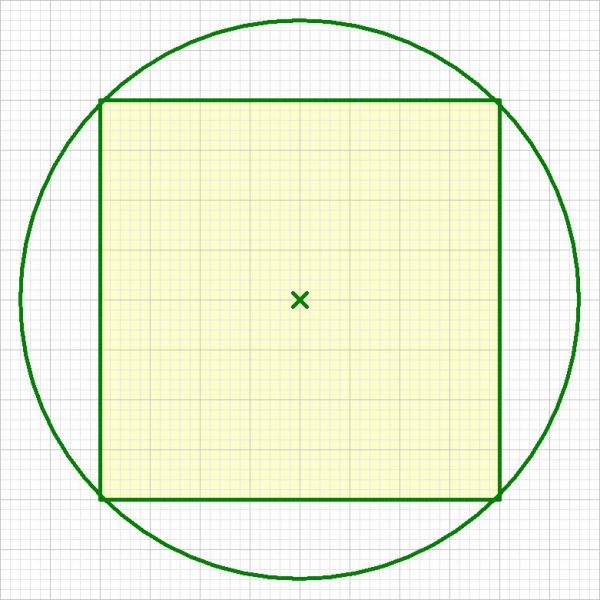
b) Vergrößert sich beim Ausklappen der Kreisteile die Tischfläche um mehr oder weniger als 50%?
Quadratfläche = 1 * 1 = 1 m^2
Kreisradius = √(0.5^2 + 0.5^2) = √0.5
Kreisfläche = pi * r^2 = pi * 0.5 = 1.571 m^2
Damit vergrößert sich die Fläche um ca. 57%
c) Bestimme den Umfang der kreisförmigen Tischplatte.
U = 2 * pi * r = 2 * pi * √0.5 = 4.443 m
d) Weise nach, dass der Anteil der Vergrößerung nicht von der Seitenlänge des Quadrats abhängt, sondern immer gleich ist.
Ich hätte das nicht in der Einheit m rechnen können sondern in jeder beliebigen Einheit. Wenn die Quadratfläche 1 km^2 ist dann ist die Kreisfläche 1.571 km^2
Damit ist die Vergrößerung nicht von der Einheit und damit nicht von der Größe abhängig.