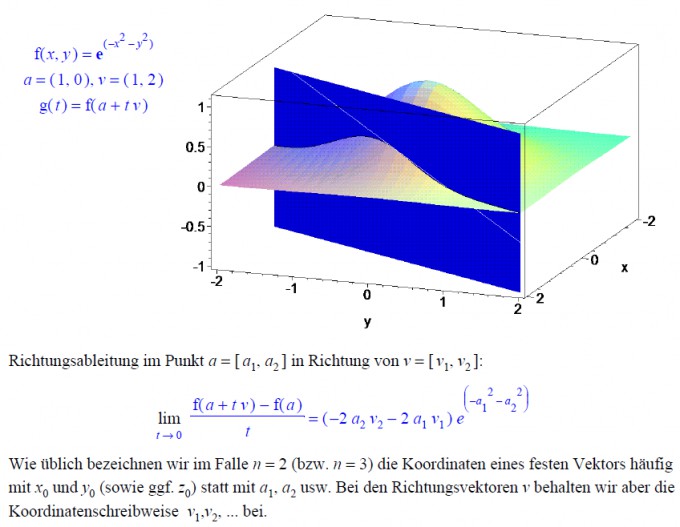
d/dx e^{-x²-y²} = -2*x*e^{-x^2-y^2}
d^2/dx^2 e^{-x²-y²} = (4*x^2-2)*e^{-x^2-y^2} {2fache Ableitung hier hast Du etwas anderes zu stehen}
d^2/dy^2 e^{-x²-y²} = (4 y^2-2)*e^{-x^2-y^2}
grad e^{-x²-y²} = (-2 x e^{-x^2-y^2}, -2 y e^{-x^2-y^2}) stimmt
Der Berg hat kein Tal (kein lokales Minimum).
Maximum sieht man leicht bei (0,0,1).
Egal in welche Richtung der Vektor zeigt {wenn er bei (0,0,0) beginnt und bei (x,y,0) endet}
das Maximum bleibt bei (0,0,1).
Punkt (-1,1): e^{-(-1)²-1²} = 1/e²=0.135335283236612691893999... hier hast Du was anderes
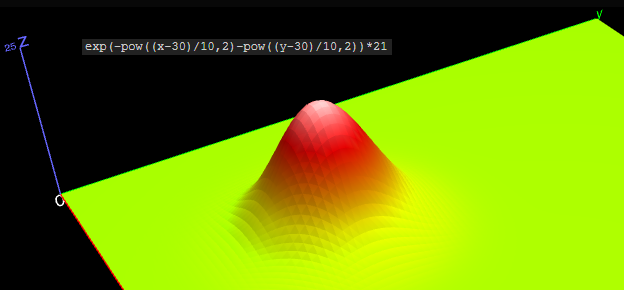
Wenn Du die 3D-Fläche ansehen möchtest:
http://www.lamprechts.de/gerd/3D-online-Plotter.htm
exp(-pow((x-30)/10,2)-pow((y-30)/10,2))*21 {absichtlich verschoben und vergrößert)
Verwirrend finde ich die Schreibweise (-1,1)^T !?
{transponiert -> vermutlich nur x,y statt nebeneinander hier übereinander}
soll das https://de.wikipedia.org/wiki/Richtungsableitung
sein?
Ohne Angabe des Startpunktes ist meist (0,0) gemeint, also a=(0,0) in dem Bild (v ist in diesem Beispiel anders, aber eine mögliche Analogie zu Deinem Beispiel):