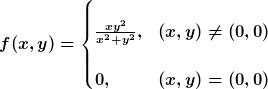
die Folge (xn , yn) = ( 1/n2 , 1/n) → (0,0) für n → ∞
für die zugehörige Funktionswertfolge gilt:
f( (xn , yn) ) = 1/n2 · 1/n2 / (1/n4 + 1/n4) = 1 / [ n2 · n2 · (1/n4 + 1/n4) ] = 1/2
sie hat also für n→∞ den Grenzwert 1/2 ≠ f( (0,0) ) = 0
→ f ist in (0,0) nicht stetig, also auch nicht differenzierbar
Gruß Wolfgang