bei a) kann man das so rechnen:
3·|x| + 4·|y| < 1 ⇔ |y| < - 3/4·|x|+ 1/4
für x ≥ 0 → |y| < - 3/4·x +1/4
für - 3/4·x + 1/4 ≥ 0 also für x ≤ 1/3 und damit für
0 ≤ x ≤ 1/3
3/4·x - 1/4 < y < -3/4·x + 1/4
für x < 0 → |y| < 3/4·x +1/4
für 3/4·x +1/4 ≥ 0 also für x ≥ -1/3 und damit für
- 1/3 ≤ x < 0
- 3/4·x - 1/4 < y < 3/4·x + 1/4
Die gesuchte Menge:
{ (x,y) ∈ ℝ2 | [ 0 ≤ x ≤ 1/3 ∧ 3/4·x - 1/4 < y < -3/4·x + 1/4 ]
∨ [ - 1/3 ≤ x < 0 ∧ - 3/4·x - 1/4 < y < 3/4·x + 1/4 ] }
grafisch sieht das dann so aus:
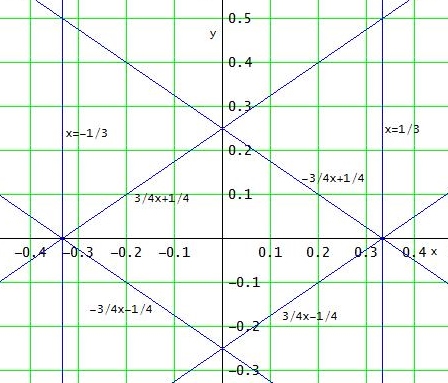
Das Parallelogramm mit dem Mittelpunkt (0|0) ist die gesuchte Menge
Gruß Wolfgang