Hallo,
ich finde die Vorstellung viel zu kompliziert ... da finde ich die Formeln im allgemeinen viel leichter.
zumindest eine qualitative räumliche Vorstellung ist IMHO unerlässlich. Auf jeden Fall vereinfacht sie das Lösen solcher Aufgaben ungemein - das ist sicher. Lernst Du nur irgendwelche Formeln (welche eigentlich?), dann wäre das so als ab Du versuchst, Fahrrad fahren zu lernen, indem Du die Anzahl der Pedalen und Speichen am Fahrrad auswendig lernst ;-)
OK - zurück zur Aufgabe: wenn ich das richtig überblicke, so fehlen noch die Aufgabenteile f) bis i)
f) Bestimme den Schnittpunkt S der Ebene E mit der Geraden g, die durch
die Punkte P(2|1|2) und Q(1|0|1) verläuft!
Die Gerade \(g\) ist$$g:\quad \vec x = P + t(Q-P)= \begin{pmatrix}2\\ 1\\ 2\end{pmatrix} + t\begin{pmatrix}-1\\ -1\\ -1\end{pmatrix}$$Frag' bitte nach, wenn Dir hier was unklar ist. Und die Ebene in Koordinatenform ist $$E: \quad 2x-4y+z=8 $$Das kann man umschreiben in die vektorielle Form (die Normalenform der Ebene)$$E: \quad \begin{pmatrix}2\\ -4\\ 1\end{pmatrix} \cdot \vec x= 8, \quad \vec x = \begin{pmatrix}x\\ y\\ z\end{pmatrix}$$das ist wirklich nur eine andere Schreibweise. Wenn Du das Skalarprodukt auf der linken Seite ausmultiplizierst, so erhältst Du unmittelbar die Koordinatenform. Dieser Vektor, der vor dem \(\vec x\) steht, ist ein Normalenvektor der Ebene \(E\). D.h. er steht senkrecht auf der Ebene, wie folgendes Bild zeigt:
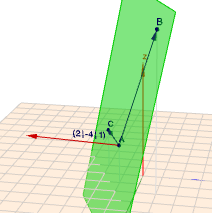
Klicke bitte auf das Bild, dann öffnet sich Geoknecht3D mit dieser Szene und Du kannst die Szene mit der Maus rotieren und bekommst so einen besseren räumlichen Eindruck.
Und um den Schnittpunkt von \(E\) und \(g\) zu berechne, setzt man für das \(\vec x\) einfach das \(g\) ein:$$\begin{aligned}\begin{pmatrix}2\\ -4\\ 1\end{pmatrix} \cdot \left( \begin{pmatrix}2\\ 1\\ 2\end{pmatrix} + t_s\begin{pmatrix}-1\\ -1\\ -1\end{pmatrix}\right) &= 8 \\ 2 + t_s \cdot 1 &= 8 \\ \implies t_s &= 8-2 = 6 \end{aligned}$$Falls Du nicht weißt, wie ich von der ersten auf die zweite Zeile komme, so frage bitte nach. Das Ergebnis ist der Wert von \(t=t_s\), für den ein Punkt auf der Gerade auch ein Punkt der Ebene ist. Um zu diesem Punkt \(S\) zu kommen, setzt man das \(t_s\) in die Geradengleichung von \(g\) ein$$ \implies S = g(t_s) = \begin{pmatrix}2\\ 1\\ 2\end{pmatrix} + (t_s=6)\begin{pmatrix}-1\\ -1\\ -1\end{pmatrix} = \begin{pmatrix}-4\\ -5\\ -4\end{pmatrix}$$Schau Dir das in folgendem Bild nochmal an (klicken)
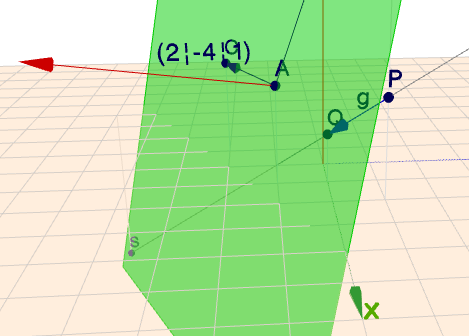
auf dem Bild kannst Du auch in etwa abschätzen, dass man die Strecke \(PQ\) \(t_s=6\)-mal zurücklegen muss, um vom Punkt \(P\) zum Punkt \(S\) zu kommen.
g) Welchen Winkel ℘ schließen g und E ein?
Für diesen Winkel brauchst Du den Normalenvektor \(\vec n\) der Ebene und den Richtungsvektor \(\vec r\) der Geraden. Ist der Winkel zwischen \(\vec n\) und \(\vec r\) gleich \(\alpha\), so ist \(℘ = 90° - \alpha\). Auch diese 'Formel' muss man nicht auswendig lernen, sondern sie folgt unmittelbar anschaulich, wenn man sich das im Detail ansieht
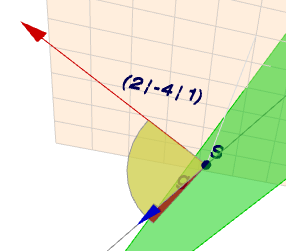
Dort siehst Du den blauen Richtungsvektor \(\vec r\) und den roten Normalenvektor \(\vec n\), den Winkel \(\alpha\) (gelb) zwischen diesen beiden Vektoren. Und daraus folgt anschaulich, dass der Winkel \(℘\) (rot) zwischen der Geraden \(g\) und der Ebene eben die Differenz von \(\alpha\) zu \(90°\) sein muss. Die Berechnung ist$$℘ = 90° - \alpha \\ \phantom{℘} = 90° - \arccos\left( \frac{\vec n \cdot \vec r}{|\vec n| \cdot |\vec r|}\right) \\ \phantom{℘} = 90° - \arccos\left( \frac{1}{\sqrt{3 \cdot 21}}\right) \\ \phantom{℘} \approx 7,2° $$
h) Welchen Abstand hat der Punkt Z1(–4|1|–1) von E?
Um den Abstand eines Punkes zu einer Ebene zu berechnen, wandelt man die Normalenform der Ebene in die Hessesche Normalenform um. Dazu teilt man die Normalenform durch den Betrag des Normalenvektors \(\vec n\), so dass der neue Normalenvektor die Länge 1 hat. Also$$|\vec n|=\left| \begin{pmatrix}2\\ -4\\ 1\end{pmatrix}\right| = \sqrt{2^2 + (-4)^2 + 1^2} = \sqrt{21} \\E: \quad \frac 1{\sqrt{21}}\begin{pmatrix}2\\ -4\\ 1\end{pmatrix} \vec x - \frac 8{\sqrt{21}} = 0$$Setzt man nun den Punkt \(Z_1\) für das \(\vec x\) in der Ebenengleichung ein, so liefert der Ausdruck den Betrag des Abstands \(e_{Z1}\):$$e_{Z1} = \left| \frac 1{\sqrt{21}}\begin{pmatrix}2\\ -4\\ 1\end{pmatrix} \begin{pmatrix}-4\\ 1\\ -1\end{pmatrix} - \frac 8{\sqrt{21}}\right| = \sqrt{21} \approx 4,58$$Auch dieser Zusammenhang folgt aus der Anschauung über das Skalarprodukt. Wenn Du mehr dazu wissen willst, so frage nochmal nach.
i) Welchen Abstand hat Z2(1|2|– 4) von g?
Wie die Abstandsberechnung zwischen Punkt \(Z_2\) und Gerade \(g\) funktioniert, kann man sich an folgendem Bild klar machen:
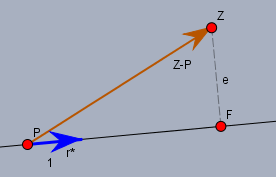
Dort siehst Du die (schwarze) Gerade \(g\) mit dem Stützpunkt \(P\) und dem normierten Richtungsvektor \(\vec r^*\) (blau) sowie dem Differenzvektor \(\vec{Z_2P} = Z_2-P\) (braun) zwischen den Punkten \(Z_2\) und \(P\). Nun ist der Abstand zwischen \(P\) und dem Fußpunkt \(F\) genau das Skalarprodukt von \(\vec{Z_2P}\) und \(\vec r^*\). Und wenn man von \(P\) nach \(F\) kommen will, so muss man also die Entfernung \(\vec{Z_2P} \cdot \vec r^*\) zurück legen. Also ist \(F\):$$F = P + \left( \vec{Z_2P} \cdot \vec r^*\right) \vec r^* \phantom{F} = P + \left( \vec{Z_2P} \cdot \frac{\vec r}{|\vec r|}\right)\frac{\vec r}{|\vec r|} \\ \phantom{F} = P + \frac{\vec{Z_2P} \cdot \vec r}{\vec r^2} \vec r$$Einsetzen der Größen gibt hier$$F = \begin{pmatrix}2\\ 1\\ 2\end{pmatrix} + \frac{6}{2} \begin{pmatrix}-1\\ -1\\ -1\end{pmatrix} = \begin{pmatrix} 0\\ -1\\ 0\end{pmatrix} $$und das Abstand ist dann \(|Z_2F| = \sqrt{26}\).
Und falls Du Fragen hast, so frage bitte.
Gruß Werner