> Wie kann ich nachweisen das für jedes a der Abstand der beiden Geraden x=xE und x=xW 1/a ist ?
Das ist nur für a>0 so.
fa'(x) = a2 ·e-ax · (1 - a·x)
fa''(x) = a3 ·e-ax · (a·x - 2)
xE = 1/a ; xW = 2/a
Die beiden Geraden x = xE und x = xW sind Parallelen zur y-Achse.
Ihr Abstand beträgt deshalb | xW - xE | = | 2/a - 1/a | = | 1/a |
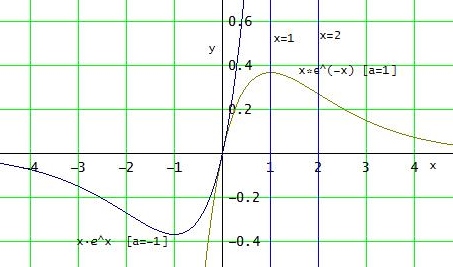
Beispiel:
Für a=1: xE = 1 und xW = 2 ; für a=-1: xE = -1 und xW = -2
Gruß Wolfgang