Danke,
Jetzt simmt auch die Probe :-).
Allerdings hab ich jetzt das Problem dass ich nicht weiss wo mein Fehler liegt. (Da ich mir eig. ziemlich sicher war dass alles richtig machte^^)
Und im ehrlich zu sein diese Potenzschreibweise verwirrt mich ein wenig.
Hier mal meine Vorgehensweise:
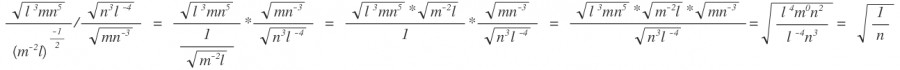
(Rechtsklick -> Grafik anzeigen; dann ists nen bissel größer; zur Not noch mit STRG * Mausrad -> zommen)