> f(x):[0,+∞] → ℝ: x →x·xx
f(x) = x · ex·ln(x) [ = x · (eln(x))x ]
a) Bestimmen Sie die Tangentengleichung von f für x0 = 1
f '(x) = ex·ln(x) · (x·ln(x) + x + 1) (Produktregel)
f '(1) = 2 ; f(1) = 1
B(1|1) ist also der Berührpunkt der gesuchten Tangent t und m = 2 ist ihre Steigung.
Die Gerade durch den Punkt P( xp | yp ) mit der Steigung m hat die Gleichung
y = m • ( x - xp ) + yp [ Punkt-Steigungs-Formel ]
t : y = 2 • (x - 1) + 1 → t(x) = 2x -1
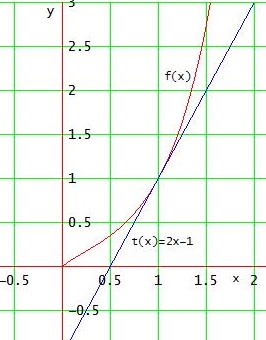
b) Approximieren Sie ∫ 0,5 1,5 f (x) dx mit Hilfe von (a)
Du sollst wohl einfach f(x) näherungsweise durch t(x) ersetzen:
0,5 ∫1,5 f(x) dx ≈ 0,5 ∫1,5 t(x) dx = 0,5 ∫1,5 (2x -1) dx
= [ x2 - x ]0,51,5 = 1,52 - 1,5 - (0,52 - 0,5) = 1
0,5 ∫1,5 f(x) dx ≈ 1 (Dreiecksfläche zwischen Tangente und Graph)
c)
Tn f(x,a) = ∑k=on f(k)(a) / k! · (x - a)k
T1 f(x,1) = ∑k=o1 f(k)(1) / k! · (x - 1)k
= f(1) / 0! · 1 + f '(1) · 1! · (x - 1)
= 1 + 2 · (x -1) = 2x -1
Das Taylorpolynom stimmt also mit der Tangente in x = 1 überein.
Gruß Wolfgang