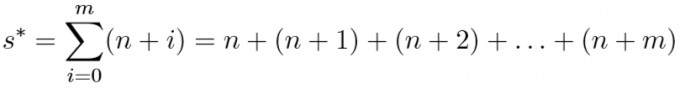
n,m∈ℕ und m ist gerade
Man soll zeigen dass die summe s* durch m+1 teilbar ist.
I.Wieso kann man obige Gleichung in diese umformen:
$$n(m+1)+\sum _{ i=0 }^{ m }{ i } $$
II. Und Wieso kann man $$\sum _{ i=0 }^{ m }{ i }$$ in$$\frac { m*(m+1) }{ 2 } $$
umformen?