Wie verändern sich die Grenzen bei der Umkehrfunktion einer Wurzelfunktion?

Question

ich habe die Grenzen 0 und 2. f(x)=3.wurzel(x). Die Umkehrfunktion ist demnach g(x)=x^3. Wie verändern sich jetzt sie Grenzen, wenn man den Flächeninhalt durch die Umkehrfunktion ausrechnen möchte bzw. muss?

Answer 1

Wenn du von 0 bis 2 schaust, dann hast du ja Punkte (x,y) und der weiteste Punkt ist der bei x=2. Wenn du dein y ausrechnest dritte Wurzel aus 2, dann weißt du deinen y-Wert. Der Punkt (0, 0) ändert sich ja nicht. Du muss also von 0 bis 3.Wurzel(2) gehen. Wurzel schreibt man auch mit x^{1/2} bzw. die dritte Wuzel dann x^{1/3}.

Answer 2

Die Fläche in den Grenzen von 0 bis 2 unter der Kurve mit der Gleichung f(x)=3.wurzel(x) kann man natürlich auch mit Hilfe der Umkehrfunktion finden. Wenn man aber die Fläche in den Grenzen von 0 bis ³√2 unter der Kurve mit der Gleichung f^-1(x)=x³ bestimmt hat, muss man diese noch vom Rechteck mit den Seitenlängen 2 und ³√2 subtrahieren (am besten Skizze machen). Dann erst hat man die gewünschte Fläche.

Comments

Hallo Roland,

ich muß meine Antwort noch deutlich nachbearbeiten.

Der Fall mit einer Umkehrfunktion die Flächen-
berechnung durchzuführen könnte dann vorkommen
falls es zu schwer ist aus der Ausgangsfunktion die Stammfunktion zu bilden.

---

... dies mit der Umkehrfunktion aber möglich wäre.

---

In meiner Antwort ist alles enthalten, was man meiner Meinung nach wissen muss, auch das Einräumen der grundsätzlichen Möglichkeit. Wenn es nicht erschöpfend ist, was ich schrieb, kann der Fragesteller natürlich nachfragen.

Answer 3

allgemein : die Integrationsgrenzen einer Funktion f
seien a und b

Die Funktionswerte seien f ( a ) und f ( b )

 

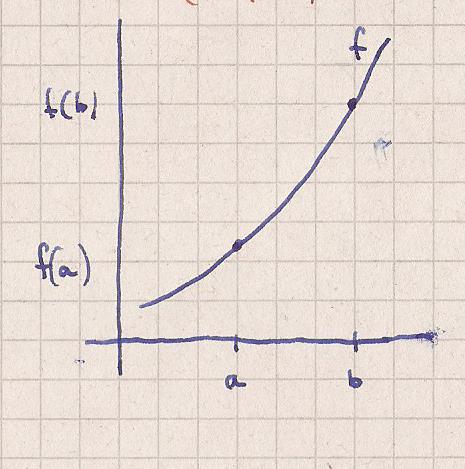
P ( x | y )
P 1 ( a | f ( a ) )
P 2 ( b | f ( b )

Für die Umkehrfunktion werden nun in den  Punkten  x
und y vertauscht

P1 ( f ( a ) | a )
P2 ( f ( b ) | b )

Für die Umkehrfunktion wird die y-Achse nunmehr
zur x-Achse.
Das Intervall geht nun von
f ( a ) bis f ( b )

Nachtrag : stimmt noch nicht vollständig.

Comments

Hier meine korrigierten Überlegungen

f ( x ) in den Grenzen a bis b wäre zu integrieren.
Dies ist die blaue Fläche.

[ ∫ f ( x ) ] _a^b

 

Die Umkehrfunktion von f nenne ich u.

Die grüne Fläche ist

[ ∫ u ( x )  ] _{f (a)} ^{f (b)}

großes Rechteck = b * f ( b )
kleines Rechteck = a * f ( a )

blaue Fläche =
großes Rechteck minus
kleines Rechteck minus
grüne Fläche