Wenn man den offensichtlichen Weg wählt, so wie mathef, dann kommt man auf zwei Gleichungen, die letztlich in einem Polynom 4'ter Ordnung enden. Das ist zwar grundsätzlich lösbar, aber vielleicht nicht so gewollt. Ich schlage daher einen anderen Weg vor, der vielleicht etwas aufwändiger ist, aber bei dem man nur eine quadratische Gleichung lösen muss.
Ich mache mir dabei zunutze, dass alle Punkte deren Summe von Abständen von \(A\) und \(B\) gleich 17,5 sind, auf einer Ellipse liegen. Dann lege ich ein Koordinatensystem derart, dass die Achsen der Ellipse parallel zu den Achsen des Koordinatensystems liegen. Die Bahnlinie ist die lineare Funktion \(y=x-5\sqrt{2}\)in diesem Koordinatensystem. Ihre beiden Schnittpunkte mit der Ellipse sind die beiden möglichen Positionen für den Bahnhof.
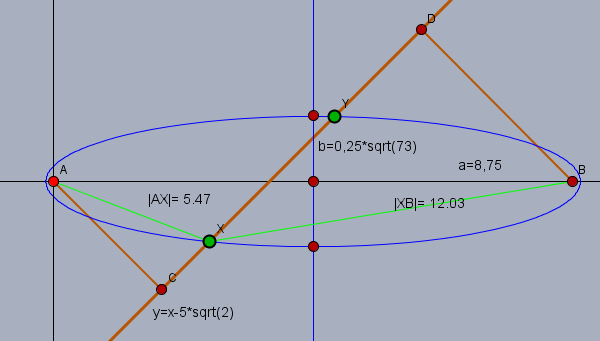
Für die Halbachse \(a\) der Ellipse muss gelten \(2a=17,5\), und da der Abstand \(AB=12\sqrt{2}\) sich leicht berechnen lässt, folgt daraus auch die Halbachse \(b=\sqrt{73}/4\). Die Ellipse ist um den halben Abstand \(AB\) nach rechts verschoben, also folgt daraus
$$\left( \frac{2(x-6\sqrt{2)^2}}{17,5}) \right)^2+ \left( \frac{4y}{\sqrt{73}} \right)^2 =1$$ Das Einsetzen der linearen Funktion (s.o.) führt zu einer quadratischen Gleichung mit den Lösungen $$x_{1}\approx 5,10127\quad x_2\approx9,19993$$ und den dazu gehörige Y-Werten $$y_1= -1,96979\quad y_2=2,12886$$ Die Strecke \(AX\) ergibt sich aus dem Pythagoras \(AX \approx\sqrt{5,10127^2 +-1,96979^2 }\approx5,4684\) und demnach ist z.B. \(CX\) $$CX\approx \sqrt{5,4684^2 - 5^2} \approx 2,2143$$
Gruß Werner