Zeichne die Funktion und die Tangente
y(x)= 1/(1-x) x_0= 2
Berechne die Steigung der Tangente im Punkt x_0/y_0
Für einen Berührpunkt gilt
f ( x ) = t ( x )
f ´( x ) = t ´( x ) | Steigung im Berührpunkt ist gleich )
f ( x ) = 1 / ( 1 - x )
f ´( x ) = 1 ( ( 1 -x ) ^2
t ( x ) = m * x + b
t ´( x ) = m
f ´( x ) = t ´( x ) | Steigung im Berührpunkt ist gleich
f ´( 2 ) = 1 / ( 1 -2)^2 = 1 = m
m = 1
f ( x ) = t ( x )
f ( 2 ) = -1
t ( 2 ) = m * x + b = 1 * 2 + b = -1
1 * 2 + b = -1
b = -3
t ( x ) = x - 3
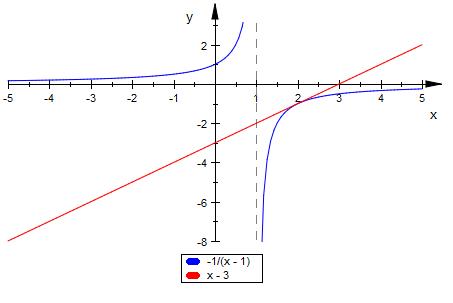
Willst du den Graph manuell zeichnen
mußt du Wertetabellen anlegen.