likeeeeeee22,
Das Kriterium für eine unitäre Matrix lautet:
$$A\cdot A^H=I\text{ mit } I = \text{ Einheitsmatrix }\wedge A^H\text{ adjungierte Matrix} $$ Sei weiterhin $$\alpha=a+b\cdot i\text{ mit }a,b\in\mathbb{R}$$ 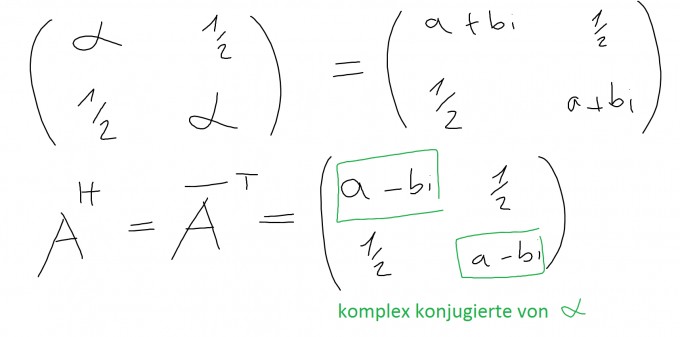
Nun bilden wir das Produkt $$A\cdot A^H$$ was die Einheitsmatrix $$\left(\begin{matrix}1&0\\0&1\end{matrix}\right)$$ ergeben soll.

Nun muss a den Wert 0 besitzen, damit die orange gefärbte Matrix die Einheitsmatrix ergibt. Weiterhin muss gelten: $$a^2+b^2+\dfrac{1}{4}=1$$ Wegen $$a=0$$ folgt $$b^2+\dfrac{1}{4}=1$$ $$\Leftrightarrow b^2=\dfrac{3}{4}$$ $$\Leftrightarrow b^2=\sqrt{\dfrac{3}{4}}$$ Die unitäre Matrix lautet mit $$\alpha=\sqrt{\dfrac{3}{4}}\cdot i\text{ also } \left(\begin{matrix} \sqrt{\dfrac{3}{4}}\cdot i & \dfrac{1}{2} \\ \dfrac{1}{2} & \sqrt{\dfrac{3}{4}}\cdot i \end{matrix}\right)$$ Diese Matrix ist unitär, was Du hier nachprüfen kannst: https://www.wolframalpha.com/input/?i=unitary+matrix+%7B%7Bsqrt(3%2F4)i,1%2F2%7D,%7B1%2F2,sqrt(3%2F4)i%7D%7D
Konnte ich Dir damit weiterhelfen? Bei Rückfragen kannst Du Dich gerne wieder melden.
André, savest8