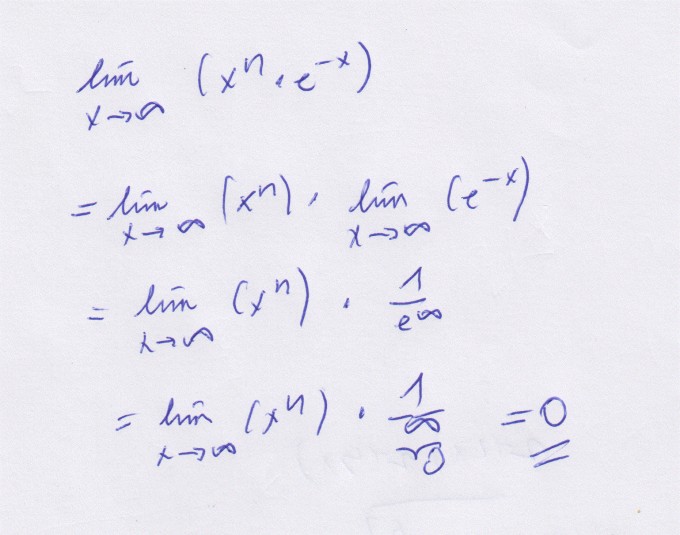Question

Wie berechne ich Schritt für Schritt lim x-->unendlich (xⁿ * e^-x) ?

Answer 1

$$\lim\limits_{x\to\infty}(x^n\cdot e^{-x})\\ =\lim\limits_{x\to\infty}(x^n)\cdot \lim\limits_{x\to\infty}(e^{-x})\\ =\lim\limits_{x\to\infty}(x^n)\cdot \frac{1}{e^\infty}\\ \lim\limits_{x\to\infty}(x^n)\cdot\frac{1}{\infty}\\ =\lim\limits_{x\to\infty}(x^n)\cdot 0 = 0$$

         

Comments

danke. kann mann hier lhospital anwenden?

---

nein das ist nicht möglich.

Answer 2

du kannst hier lhospital n-mal anwenden.

Comments

.. und wünsche dir dafür ein langes Leben, wenn z.B.  n = 35441877452  ist.

---

Die Größe von n ist hierbei unbedeutend.