Quadrik Q={x ∈ R2| x^{⊺} Ax + 2a^{⊺}x +c=0} mit A=((8,0),(0,2)),a=(1,6,2),c=26 euklidische Normalform

Question

Gegeben ist die Quadrik Q={x ∈ R2| x^{⊺} Ax + 2a^{⊺}x +c=0} mit
A=(8002),a=(162),c=26


(a) Bestimmen Sie eine euklidische Normalform von Q.

(b) Skizzieren Sie die Quadrik Q in Standardkoordinaten.
Zeichnen Sie zudem das
Koordinatensystem ein, welches zur oben bestimmten
euklidischen Normalform gehört.

Wie Bestimme ich die euklidische Normalform?

Ausführlich bitte undzwar die Rechenschritte bitte.

Freundliche Grüße

immai

EDIT: Überschrift Nun Quadrik Q={x ∈ R2| x^{⊺} Ax + 2a^{⊺}x +c=0} mit A=((8,0),(0,2)),a=(1,6,2),c=26 euklidische Normalform

Versuch die Formatierung zu rekonstrieren. 

Comments

EDIT: Überschrift Nun Quadrik Q={x ∈ R2| x^{⊺} Ax + 2a^{⊺}x +c=0} mit A=((8,0),(0,2)),a=(1,6,2),c=26 euklidische Normalform

Versuch die Formatierung zu rekonstrieren. (??) Welche Komponenten hat a? 

---

Sag mal, die Aufgabenstellung ist doch schon falsch. \( x \in \mathbb{R^2} \) und \( a \in \mathbb{R^3} \) ? da stimmen doch die Dimensionen noch nicht mal. Ein bisschen mehr Genauigkeit bitte!

---

R^{2}

Ist schon richtig der rest steht nicht schön.

Hier die bild datei indemfall.

---

Kann mir hier einer weiter helfen bitte

---

ich brauche die aufgabe bis morgen

bitte ausrechnen^^

Vielen Dank

immai

Answer 1

EW 8,2

Drehung/Rotation

\(\small R \, :=  \, \left(\begin{array}{rr}0&-1\\1&0\\\end{array}\right)\)

Verschiebung/Trans

\(T \, :=  \, \left\{ x = x - 1, y = y + \frac{13}{4}  \right\} \)

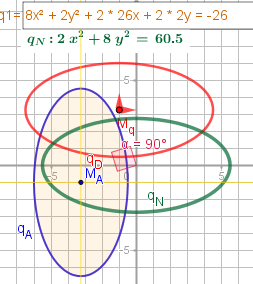
Man könnte

\(q_A(x, y) \, :=  \, 8 \; x^{2} + 2 \; y^{2} + 52 \; x + 4 \; y + 26\)

auch einfach Verschieben (quad. Ergänzen)

q_N:=q_A(x - 13/4,y - 1 )=0

\(q_N:=8 \; x^{2} + 2 \; y^{2} - \frac{121}{2} = 0\)