Wie bekommt hier den Flächeninhalt raus?

Question

Wie berechnet man den Inhalt der Fläche die der Graph von f mit der x-Achse einschließt ?

 f (x) = x⁴-4x²

Waß bekommt hier zunächst für =x und wie bekommt man die Stammfunktion und wie lautet dann der Rechenweg?

Vielen Dank

Answer 1

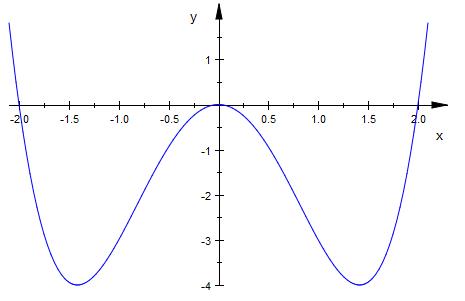
f (x) = x⁴-4x²

Nullstellen
x⁴ - 4*x² = 0
x² * ( x² - 4 ) = 0
x = 0
und x² -4 = 0
x = +2
x = -2

Stammfunktion
S ( x ) = x⁵ / 5 - 4 * x³ / 3

Aufgrund der geraden Exponenten ist die Funktion
Achsensymmetrisch zur y-Achse.

Es brauchtr nur die Fläche zwischen 0 und 1
berechnet zu werden.

[ S ( x ) ]  zwischen 0 und 2

- 64 / 15
als Fläche 64 / 15
und das mal 2
128 / 15

mfg Georg

Answer 2

Die Nullstellen sind -2, 0, +2. die Stammfunktion F(x)=x⁵/5-4/3x³. Jetzt die Beträge von F(0)-F(-2) und F(2)-F(0) addieren.