Wie berechnet man hier den Flächenwert der Funktion von [a;b]?

Question

ich habe eine Frage zum Hauptsatz der Integralrechnung F [a-b] = F[b] - F[a] bei der folgenden Funktionsskizze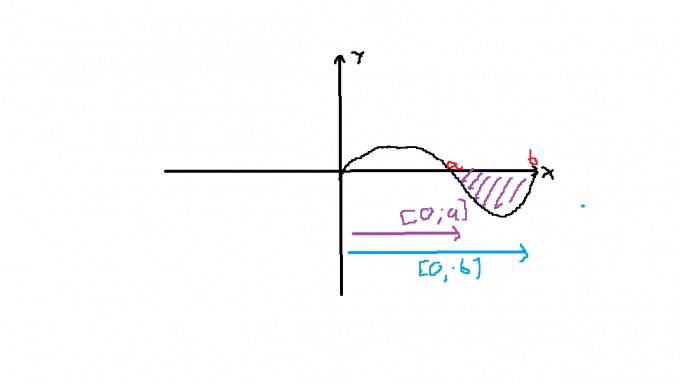 

a und b seien die Nullstellen. Um F[a-b] zu berechnen, muss ich ja F(a) von F(b) abziehen und dazu muss ich erstmal F(b) berechnen, also die Fläche von 0 bis b.

Aber hier heben sich ja positive und negative Flächen auf. D.h., dass ich nicht den tatsächlichen Flächenwert von [0;b] erhalte. Daher erhalte ich doch bei der Rechnung F[b] - F[a] auch nicht den tatsächlichen Flächenwert von a-b, sondern die Summe aus der negativen und positiven Teilfläche.

Was muss ich also tun, um den Flächenwert F[0-b] zu berechnen ohne dass sich die Flächen aufheben, damit ich den Hauptsatz der Integralrechnung anwenden kann?

Oder kann man hier auch ganz normal einfach F(b) - F(a) rechnen?

Danke.

Answer 1

Oder kann man hier auch ganz normal einfach F(b) - F(a) rechnen?

Kannst du immer machen wenn zwischen a und b keine Nullstellen sind,

und das ist ja hier der Fall.

Am Ende ggf. den Betrag nehmen.

Comments

Aber um F(a,b) zu berechnen, muss ich ja erstmal F(b) berechnen und davon F(a) abziehe

Und wenn ich F(0-b) rechne (also in den Taschenrechner in die Gleichung b einsetze), was kommt dann für diese Funktion raus? Die tatsächlcihe Fläche zwischen 0 und b oder die Summe der positiven und negativen? Wenn nicht die tatsächliche Fläche rauskommt, dann kann ich ja auch nicht  Das Ergebnis benutzen um F[a;b] zu berechnen oder?

---

Du meinst ja sicher: Für F nimmst du irgendeine Stammfunktion

von f.

Da sagt sowas wie F(b) alleine noch gar nichts.

Davon gibt es ja auch viele.

Nur die Differenz  F(b) - F(a) liefert das Integral, also die

gesamte Bilanzsumme von a bis b .

Und wenn zwischen den beiden keine Nullstelle von f mehr ist,

dann entspricht das dem Flächeninhalt.

Answer 2

Flächen sind immer nur von Nullstelle zu Nullstelle
zu berechnen.

Ich setze  sin ( x ) einmal für die Funktion

∫ sin ( x ) dx  zwischen 0 bis a
und
∫ sin ( x ) dx  zwischen a bis b

Beide Ergebnisse absolut setzen und addieren
ergibt die Fläche von 0 bis b.

mfg Georg