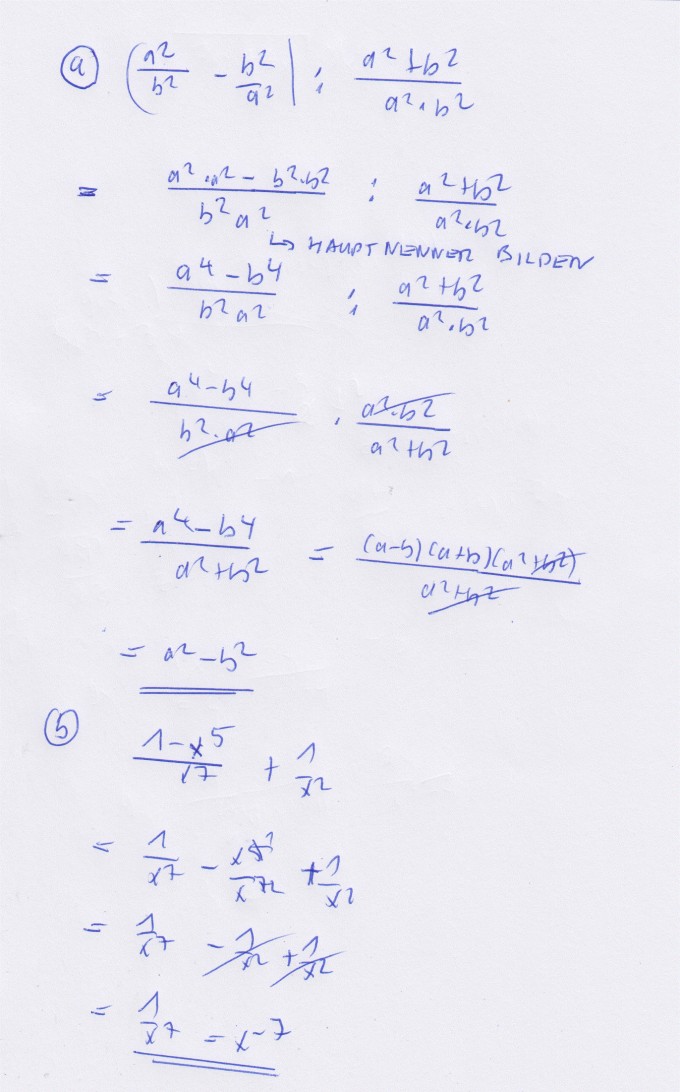Terme mit Potenzen vereinfachen

Question

Wie kann man diese Terme mit Potenzen vereinfachen?

a) \( \left(\frac{a^{2}}{b^{2}}-\frac{b^{2}}{a^{2}}\right): \frac{a^{2}+b^{2}}{a^{2} \cdot b^{2}} \)
b) \( \frac{1-x^{5}}{x^{7}}+\frac{1}{x^{2}} \)
c) \( \frac{a^{-4} b^{5}}{x^{-3} y^{-2}} \cdot \frac{x^{-2} y^{-1}}{a^{-3} b^{6}} \)
d) \( \frac{p^{2}+p \cdot q}{\left(u^{2}-r^{2}\right)^{4}} \cdot \frac{(u+v)^{4}}{p^{2}-q^{2}} \)
e) \( 25 \cdot 2^{n+2}+28 \cdot 2^{n} \)
f) \( x \cdot y^{n+2}-\left(x \cdot y^{2}\right)^{n}+\left(\frac{x}{y^{-2}}\right)^{n} \)
g) \( -\frac{1}{\left(x \cdot y^{n+2}\right)^{-1}} \)

Answer 1

Aufgabe a:

\( \left(\frac{n^{2}}{b^{2}}-\frac{b^{2}}{a^{2}}\right): \frac{a^{2}+b^{2}}{a^{2}+b^{2}} \)
\( \begin{array}{l} {=\frac{a^{2}+a^{2}-b^{2} \cdot b^{2}}{b^{2} a^{2}}: \frac{a^{2}+b^{2}}{a^{2}+b^{2}}} \\ {=\frac{a^{4}-b^{4}}{b^{2} a^{2}}: \frac{a^{2}+b^{2}}{a^{2}, b^{2}}} \end{array} \)
\( a^2 - b^2 \)

Aufgabe b:

\(\begin{aligned} & \frac{1-x^{5}}{x^7}+\frac{1}{x^{2}} \\=& \frac{1}{x^{7}}-\frac{x^{5}}{x^{7}}+\frac{1}{x^{2}} \\=& \frac{1}{x^{7}}-\frac{1}{x^{2}}+\frac{1}{x^{2}} \\=& \frac{1}{x^{7}}=x^{-7} \end{aligned}\)

Comments

Wie kommst du bei der ersten Aufgabe darauf dass im Zähler a²*a^2-b²*b² und unten halt b²*a² steht?

Und bei der anderen Aufgabe wie kommt man darauf das dann aus diesem Bruch 1/x² steht?

---

1. Ich habe den Hauptnenner gebildet.

2. Allgemein gilt: (A-B)/C= A/C -B/C