f(x) = 1/2·(2·x^4 - 5·x^2 + 4) = x^4 - 2.5·x^2 + 2
f'(x) = 4·x^3 - 5·x
F(x) = 1/5·x^5 - 5/6·x^3 + 2·x
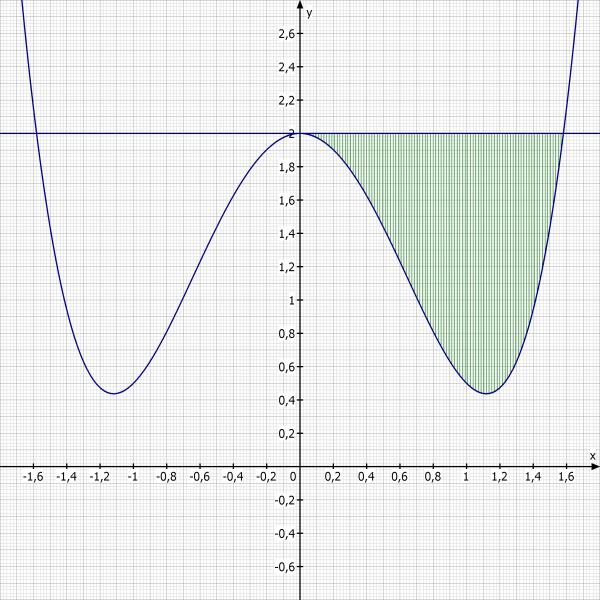
Die Tangente ist an der Stelle 0
t(x) = f'(0)·(x - 0) + f(0) = 2
Bilden der Differenzfunktion
d(x) = f(x) - t(x) = x^4 - 2.5·x^2
D(x) = x^5/5 - 5·x^3/6
Schnittstellen
d(x) = x^2·(x^2 - 2.5) = 0
x = 0 ∨ x = √2.5 (Negative Lösung interessiert mich hier nicht)
D(√2.5) - D(0) = (- 5·√10/12) - 0 = - 5·√10/12 = -1.317615691
Die Fläche beträgt ungefähr 1.318 FE
Skizze: