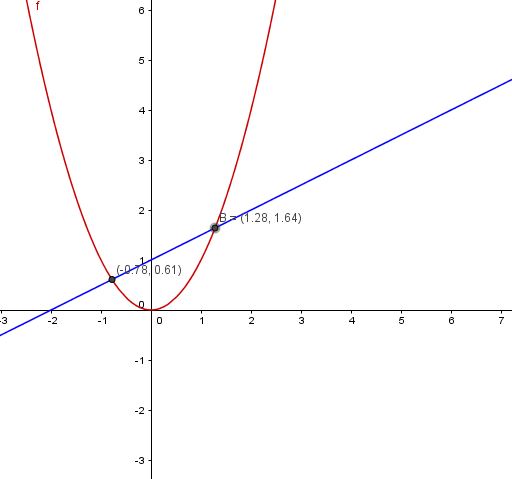
Der Ansatz, die Ungleichung als Gleichung zu schreiben, ist richtig. Du erhältst dann
x2 = 0,5x + 1 Ι -0,5x und -1
x2 -0,5x - 1 = 0
Nun wird die pq-Formel angewendet
x1/2 = 0,25 ± √0,252 +1
x1 = 0,25 + 1,03 = 1,28 und x2 = 0,25 - 1,03 = -0,78
Wenn du dir dann die Skizze anschaust, ist klar, dass x > 1,28 und kleiner als -0,78