Die Abbildung auf injektivität und Surjektivität untersuchen: x -> (x-1)/(1+x^2) R -> R

Question

 

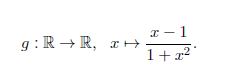
also erstmal ableiten dann sehe ich, dass die Funktion ein minimum hat also kann sie ja nicht injektiv sein, 

dazu kann ich auch als beweiß einfach ein Gegenbeispiel mit y=-1 bringen, denn dann kommt 0=x2+x was ja Unsinn ist also nicht surjektiv... 

Aber wie kann ich genau injektivität zeigen? ich bekomme irgendwie keine Umkehrfunktion hin.

da kommt nur Quatsch bei mir raus... 

mfg

Answer 1

Tipp: Es gilt ƒ(0) = ƒ(-1).

Comments

Danke dir und mir fällt grad auf,dass ich den Beweis für die Surjektivität auch brauche denn das was ich meinte ist ja eigentlich Injektivität. 

Mfg

---

Zeige z.B., dass die Gleichung ƒ(x) = 1 keine reelle Lösung für x hat.

Answer 2

Wenn du Extrempunkte bestimmst, siehst du, dass es ein Min und ein Max gibt.

In der Nähe davon gibt es x-Werte mit gleichem Funktionswert, also nicht Injektiv.