Du hast es hier mit einer Exponentialgleichung zu tun. Es gibt nur eine Unbekannte und nur eine Gleichung, deshalb ist das kein Gleichungssystem (habe das in deiner Frage entsprechend korrigiert).
e0.5x+e-0.5x=4
Substituiere: u = e0.5x
Dann hast du
u + 1/u = 4
u^2 - 4u + 1 = 0 | Quadratische Gleichung!
u = 1/2 ( 4 ± √(16 - 4))
u = 1/2 (4 ± 2√(3))
u = 2 ± √3
Nun erst mal nachrechnen, rücksubstituieren und x bestimmen.
Zur Kontrolle am Schluss:
https://www.wolframalpha.com/input/?i=e%5E(x%2F2)%2Be%5E(-x%2F2)%3D4
Beachte auch, dass der cosh(x) in deiner Gleichung versteckt ist. Mit arcosh(...) bist du noch schneller am Ziel.
"alternate form" hier: https://www.wolframalpha.com/input/?i=cosh(x)

==> cosh(x/2) = 2
https://www.wolframalpha.com/input/?i=cosh(x%2F2)+%3D+2
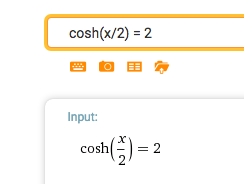
x/2 = ± arcosh(2) | Symmetrie von arcosh nicht vergessen !
x = ± 2 arcosh(2)
