ich komme leider nicht hier weiter. Kann mir jemand den Rechenweg erklären und eine kurze Erklärung dazu abgeben?
___________________________________________________________
Bestimmen Sie die Defintionslücken sowie die stetige Forsetzung von f mit
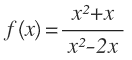
f\left( x \right) =\frac { x²+x }{ x²-2x }
___________________________________________________________