Hallo Marion,
> Die Parabel hat im Ursprung ein Extremum und hat den Wendepunkt W(4 / -128/3). Wo liegt der Tiefpunkt von f?
Der Graph einer Parabel 3. Ordnung liegt symmetrisch zum Wendepunkt.
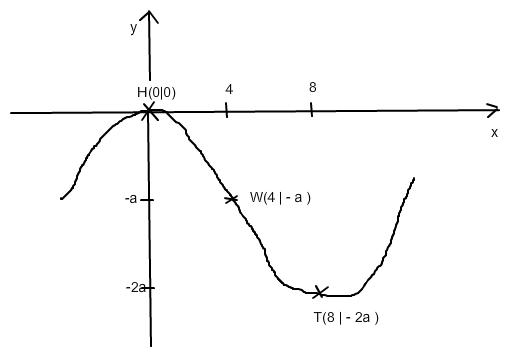
Deshalb ist (0|0) der Hochpunkt, und der Tiefpunkt ist
T( 2*4 | 2 * (-128/3) ) = T(8 | -256/3) )
Gruß Wolfgang