Parabeln und Funktionsgleichung

Question

Aufgabe:

Gegeben sind jeweils verschiedenen Parabeln, bestimme rechnerisch die Funktionsgleichung.Die Parabel hat den Scheitel auf der y Achse und verläuft durch P(2/3) und Q(-4/0)

Problem/Ansatz:

Verstehe gar nicht wie ich diese Punkte in eine Formel bringen soll und auch nicht welche Formel ich anwenden muss.

Comments

Welcher Schlaumeier sieht denn zur verlinkten Frage ein Duplikat? Es gibt zwar ein bereits beantwortetes Duplikat, aber das ist eine andere Frage und nicht die verlinkte...

Answer 1

Das ist eine sogenannte Steckbriefaufgabe.

Ansatz

f(x) = ax² + bx + c

Bedingungen in mathematischer Kurzform und das Gleichungssystem.

b = 0
f(2) = 3 --> 4a + 2b + c = 3
f(-4) = 0 --> 16a - 4b + c = 0

Errechnete Funktion

f(x) = -0,25·x² + 4

Answer 2

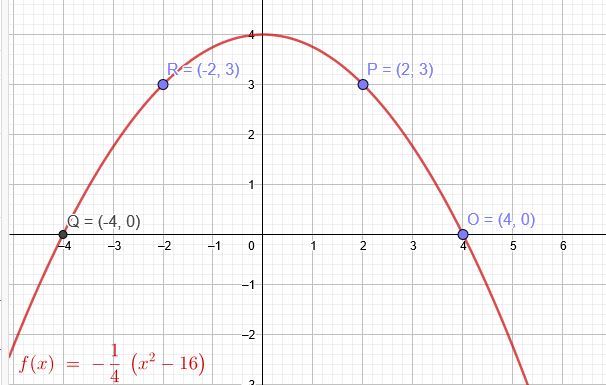
Die Parabel hat den Scheitel auf der y Achse und verläuft durch $P(2|3)$ und $Q(-4|0)$

Bedingt durch die Symmetrie zur y-Achse gilt auch:  $P(2|3)$  →   $R(-2|3)$    und  $Q(-4|0)$   →  $O(4|0)$

$f(x)=a(x+4)(x-4)=a(x^2-16)$

$P(2|3)$:

$f(x)=a(4-16)=-12a=3$

$f(x)=a(4-16)=-12a=3$   →  $a=-\frac{1}{4}$

$f(x)=-\frac{1}{4}(x^2-16)$