ich rechne die Aufgabe in GeoGebra und kommentiere die Rechenschritte
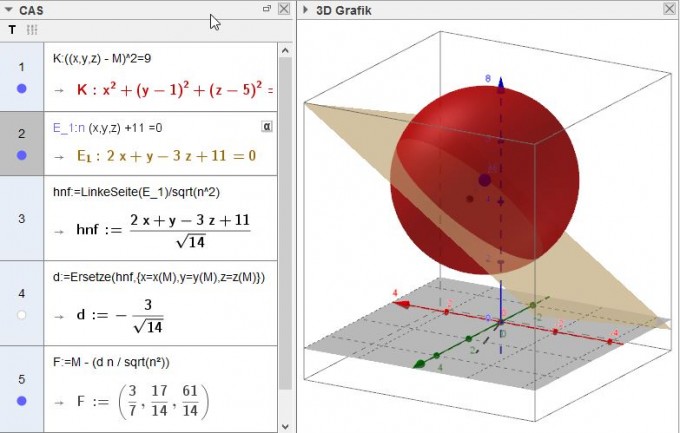 Festlegungen:
Festlegungen:
Kugelmittelpunkt M=(0,1,5)
Normalenvektor E_1 n=(2,1,-3)
1: Vektorschreibweise der Kugelgleichung
2. Vektroschreibweise der Ebenengleichung
3: HNF: Teile E_1 durch den Betrag des Normalenvektors um
4: den Abstand (mit Vorzeichen) des Kugelmittelpunktes von der Ebene zu bestimmen
setze M in HNF ein - für x=0, y=1, z=-3
|d| = r Berührpunkt, |d|>r vorbei, |d|<r Schnittkreis ( 0.8 < 3 hammer hier)
5: Maschiere von M in (Gegen)Richtung des (normierten) Normalenvektors die Strecke d (mit Vorzeichen) zur Ebene - dort findest Du der Schnittkreismittelpunkt F
Ersatzweise kannst Du aus M und dem Normalenvektor eine Gerade machen und den Schnittpunkt mit E_1 berechnen...