Du kennst sicher die Formel zur Berechnung des Flächeninhalts eines Kreises - der Flächeninhalt sei \(A\) und der Radius des Kreises sei \(r\). Dann ist der Flächeninhalt in Abhängigkeit des Radius \(r\):
$$A(r)=\pi \cdot r^2$$
Die Änderungsrate ist die Änderung des Flächeninhalts bei einer Änderung von \(r\) - also die Ableitung von \(A(r)\) nach \(r\) - und das ist ganz formal:
$$\frac{d}{dr}A(r)=2\pi \cdot r$$
Zur geometrischen Interpretation eine Skizze:
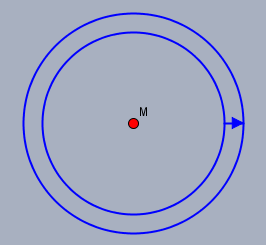
Wenn der Radius eines Kreises um einen geringen Betrag wächst - hier dargestellt durch den kleinen blauen Pfeil - dann wächst seine Fläche um die dargestellte Ringstruktur. Und die ist natürlich umso größer, desto größer der Ausgangsradius vorher schon war. Wenn man sich die Ändrung ganz klein vorstellt, dann ist der Flächenzuwachs doch gleich dem Delta, um das der Radius wächst, mal die Länge der Rings. Und diese Länge ist doch gleich dem Umfang.
Und der Umfang eines Kreises ist bekanntermaßen
$$U(r)=2\pi \cdot r$$
Na - kommt Dir das bekannt vor (s.o.)?