Flächensätze im rechtwinkligem Dreieck

Question

Hallo könnte mir jemand mit der Aufgabe Nummer 4) weiterhelfen danke:)

Comments

EDIT: Bitte Text auch als Text eingeben: https://www.mathelounge.de/schreibregeln

Answer 1

Kathetensatz: a²=3a/5·50. Umformen a²-30a=0. Ausklammern a(a-30)=0. Satz vom Nullprodukt a=0 oder a=30..

Answer 2

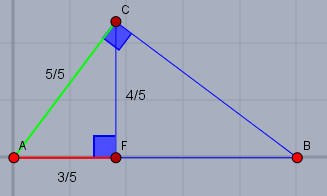
\(q=AF\), \(b=AC\) und \(c=AB\). Wegen der Kongruenz der Dreiecke \(ABC\) und \(AFC\) gilt

$$\frac{q}{b}=\frac{b}{c}$$

mit \(q=\frac{3}{5}b\) erhält man

$$b^2=q\cdot c=\frac{3}{5}b \cdot c \quad \Rightarrow \space b=\frac{3}{5}c=30\text{cm}$$

Und die Seite \(a=BC\) folgt dann aus dem Pythagoras \(a^2+b^2=c^2\). \(a=40\text{cm}\).

Answer 3

Nach dem Kathetensatz gilt:

$$ a^2 = c·p \\a^2 = 50·\frac{3}{5}·a \\a^2 = 30a \\a^2 - 30a = 0 \\a·(a - 30) = 0 \\⇒ a = 0 ∨ a - 30 = 0 ⇒ a = 30 $$

Nach dem Satz des Pythagoras ist

$$ b = \sqrt{c^2 - a^2} \\ b = \sqrt{50^2 - 30^2} = 40 $$