Willkommen in der Mathelounge!
Ich weiß natürlich nicht, was auf dem Blatt 4 der Vorlesung 5 steht. Ich versuche es mal über die Symmetrie.
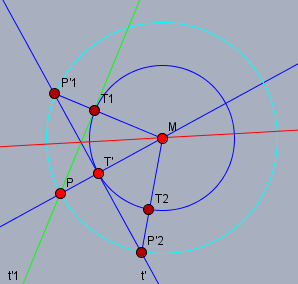
Man füge die Winkelhalbierende \(a\) (rot) von \(P'_1M\) und \(PM\) ein. Dann ist \(P\) der Bildpunkt zu \(P'_1\) und \(T_1\) der Bildpunkt zu \(T'\) bezogen auf die Symmetrieachse \(a\). Daraus folgt, dass die Gerade durch \(PT_1=t'_1\) (grün) die Bildgerade zu \(t'\) ist. Gleichzeitig ist der Kreis \(K\) das Bild seiner selbst. Und da \(t'\) Tangente an \(K\) ist, muss demzufolge auch \(t'_1\) Tangente an \(K\) sein.
Mit der gleichen Argumentation kann man belegen, dass die Gerade durch \(PT_2\) Tangente an \(K\) ist. Und da es nur zwei Tangenten von \(P\) an \(K\) geben kann, berühren die Tangenten von \(P\) an \(K\) den Kreis \(K\) in \(T_1\) und \(T_2\).
Gruß Werner