Bleibt der Index k bei 1 oder läuft er gegen n also gegen unendlich?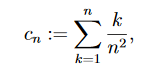
Nach meinen Berechnungen sind die ersten Werte:
c1= 1
c2= 1+ 2/4 =3/2
c3= 3/2 + 3/9 = 33/18
Liege ich hier richtig? wenn ja müsste die Folge doch gegen undendlich laufen? Ich wüsste nicht wie der Grenzwert sonst bestimmt werden kann