Es heisst:
Determinante einer (2,2)-Matrix
Jeder quadratischen Matrix wird ihre Determinante - eine Zahl - zugeordnet.
Für (2,2)-Matrizen (zweireihige Matrizen) ist sie wie folgt definiert:Dann wird die Determinante einer (3,3)-Matrix definiert.
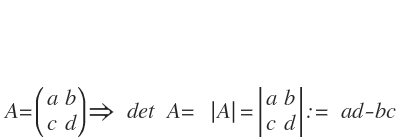
Flächenberechnung im R^{2}

(Bemerkung: Ich musste den Text im Editor schreiben weil ein Vektor in der Spaltenform während des Textes vorkommt)
Meine Frage
Ich weiss jetzt, was Matrizen sind, bei mir kommen sie Hauptsächlich in der Analytischen Geometrie vor. Weiter weiss ich von Videos dass es das Gaussche-Auflösen einer solchen Matrize gibt mit der Man Gleichungssysteme lösen kann indem man die Koeffizienten auflistet.
Okay, also hab ich Probleme in der Mathematik bei denen ich Matrizen beiziehen muss. Weil ich jetzt einzelne Sachen in Matrizen darstelle, gibt es auch Rechengesetze für soclhe Matrizen.
Ist also die Determinante auch so quasi ein "Rechengesetz" im Bezug auf die Matrizen?
Es gibt ja im Bezug auf Vektoren das Skalarprodukt, die Addition etc. ist die Determinante auch eine - ich würd dem jetzt wahrscheinlich fälschlicherweise Rechengesetz sagen- Regel die man im Bezug auf jegliche Matrizen anwenden kann, im Falle der Vektoren, liefert die Determinante praktischerweise den Flächeninhalt eines Parallelogramms.