Berechne die Hypotenuse.

Question

 Also ich hab schon mal die höhe ausgerechnet. (h=5,66) Und ich weiß, dass die formel h2=p*q ist Aber weiter kann ich nicht kann mir da jemand helfen?

EDIT: Kopie aus Kommentar: Also die eigentliche Aufgabe lautet: Gegeben sind eine 6 cm lange Kathete eines rechtwinkligen Dreiecks und der dazugehörige 2cm lange Hypotenusenabschnitt. So und die Höhe hab ich ja Also ich denke ja dort müsste ein rechter Winkel sein.

Comments

Was ist denn die Aufgabe?

---

Warum Hypotenuse?

Hast du oben einen rechten Winkel zeichnen wollen?

---

Also die eigentliche Aufgabe lautet: Gegeben sind eine 6 cm lange Kathete eines rechtwinkligen Dreiecks und der dazugehörige 2cm lange Hypotenusenabschnitt. So und die höhe hab ich ja Also ich denke ja dort müsste ein Rechter winkeö sein.

---

Aus der Aufgabe sollte schon hervorgehen, was eigentlich gesucht ist, oder etwa nicht? Und mit wie vielen Hs schreibt man das H-Wort?

---

Ich verstehe nicht?..

---

Das bild ist leider fehlerhaft.

2 cm ist ein Hypotenusenabschnitt und damit sollte der obere Winkel ein rechter sein.

http://www.arndt-bruenner.de/mathe/scripts/dreiecksberechnungrw.htm

Achtung: p und q sind auf obiger Seite eventuell anders definiert.

Answer 1

b = 6

q = 2

h = √32

p = 16

c = 18

a = √288

Comments

aber eine frage kannst du mir den rechenweg von c zeigen also wie man das mit h²=p*q macht..

---

Man muss ja glaub ich 5,66²=2*p und dann keine ahnung..

---

p * q = h^2

p = h^2 / q

p = 32 / 2 = 16

Answer 2

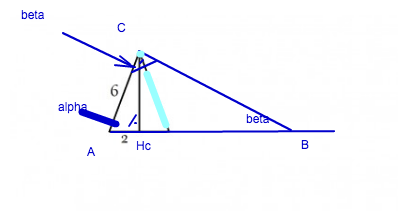
Gegeben sind eine 6 cm lange Kathete eines rechtwinkligen Dreiecks und der dazugehörige 2cm lange Hypotenusenabschnitt. Berechne die Hypetenuse. 

Das die korrigierte und ergänzte Skizze. Die gesuchte Hypotenuse ist die Seite c in Dreieck ABC.

Die beiden Dreiecke AHcC und ABC haben die gleichen Winkel (Winkelsumme im Dreieck ist 180°). Die beiden Dreiecke sind zueinander ähnlich. Daher stimmen einander entsprechende Seitenverhältnisse miteinander überein.

Bsp.

Hypotenuse : (kürzere Kathete)

Grosses Dreieck … kleines Dreieck links

c : 6 = 6 : 2              Verhältnisgleichung | * 6

c = 6*6/2 = 18  Einheit cm nicht vergessen.

Answer 3

Deine Skizze ist falsch weil der obere Winkel
des großen Dreiecks nicht 90 ° beträgt.
Lu´s Skizze ist richtig.
Die Kathete und der Hypotenusenabschnitt
des großen Dreiecks wandeln sich für den
linken Teil ( kleines Dreieck ) zur
Hypotenuse 6 cm
Kathete 2 cm
Pythagoras
6^2 = 2^2 + h^2
h^2 = 36 - 4
h = 5.66 cm

Weiter geht es im großen Dreieck mit dem Höhensatz
des Euklid

p * q = h^2
2 * q = 32
q = 16

Insgesamt c = p + q = 16 + 2 = 18 cm

Comments

Könntest du mir h²=p*q genauer erklären also den rechen weg Zb. mit der Äquivalenzumformung..?

---

Hier eine richtige Skizze aus

http://www.frustfrei-lernen.de/mathematik/kathetensatz-hoehensatz-euklid.html

Bitte frage solange nach bis dir die
Aufgabe klar ist.

Die Strecke CS ist die Höhe h.
Pythagoras
b^2 = g^2 + h^2
6^2 = 2^2 + h^2
h^2 = 36 - 4 = 32
h = √ 32
h = 5.66 cm

Für das große Dreieck wird der Höhensatz des
Euklid angewendet

q * p = h^2
2 * p = 32
p = 16 cm

mfg Georg