Partielle Ableitungen einer abschnittsweise definierten Funktion f.

Question

Betrachte die Funktion f : ℝ² → ℝ gegeben durch

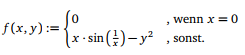
a) Gebe die partiellen Ableitungen von f an, für alle Punkte (x, y) ∈ ℝ² mit x≠0.

b) Existieren auch die partiellen Ableitungen ∂x f (0, y) bzw. ∂y f (0, y), für beliebige y ∈ ℝ? Wenn ja, gebe diese an.

Bei der a) müssen wir ja wegen x≠0 nur die partiellen Ableitungen von f(x,y):= x * sin(1/x) - y² finden.

Und diese wären f_x(x, y)= sin(1/x) - cos(1/x) * 1/x  und f_y(x, y)= -2y

Die b) verstehe ich jedoch nicht. Was bedeutet ∂x f (0, y) und ∂x f (0, y) und wie löse ich b)?

Danke :)

Answer 1

Was bedeutet ∂x f (0, y) und ∂x f (0, y) und wie löse ich b)?

Am besten nach der Def:

Für  ∂x f (0, y)  betrachtest du  den Grenzwert

für x gegen 0 von

( f(x,y) - f(o,y) ) / x

= (x*sin(1/x) - y^2 ) / x

= sin(1/x) -  y^2 ) / x

Der Gw existiert micht, also auch kein ∂x f (0, y) .

   Für  ∂y f (0, y)  (so soll es ja wohl heißen !) 

den  GW für h gegen 0 von

( f(0,y+h) - f(o,y) ) / h

= ( 0 - 0 ) / h

Und das ergibt 0, also ist  ∂y f (0, y)  = 0 .