Funktion auf Stetikgeit prüfen im f1: R->R, f1(x):= x^2 cos(2x-1) + 42 (keine konkrete x-Stelle)

Question

 

ich stecke momentan in der Vorbereitung einer Mathe-Prüfung. Generell weiß ich wie man Funktionen auf Stetigkeit überprüft. Nun bei dieser Aufgabe geht es um eine Funktion die von ℝ→ℝ abgebildet wird.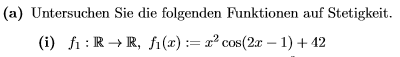 

Ich hab mir schon dazu Gedanken gemacht und bin darauf gekommen, dass die Funktion stetig ist aus dem Grund, das man keine Einschränkung hat, "alles" einsetzten darf und "alles" rauskommen kann. Das kommt mir aber zu einfach vor. 

Vielleicht kann mich ja einer aufklären.  

Habdaeinefrage

Comments

Verwende bekannte Sätze zur Stetigkeit.

Answer 1

Hallo HdeF,

f(x) = x² · cos(2x-1)  

die Funktionen mit x ↦_ℝ  x²  und  x ↦_ℝ  2x-1  sind als rationale Funktionen stetig.

Die Kosinusfunktion ist ebenfalls stetig.

→ x ↦_ℝ  cos(2x - 1)  ist als Hintereinanderausführung (Komposition) stetiger Funktionen                                         stetig.

→  x ↦_ℝ  f(x)  ist als  Produkt  stetiger Funktionen stetig. 

Gruß Wolfgang