auf einer vollen rolle sind 10000 aufkleber wieviel aufkleber sind auf der halben rolle

Question

auf einer vollen rolle Außendurchmesse = 40 cm Innendurchmesse = 8 cm sind 10.000 Stück Etiketten

wie berechne ich wieviel Etiketten es noch bei 20 cm oder 10 cm sind?

danke im voraus

gruß bernd

Answer 1

Ich würde es im Verhältnis der Flächen der Kreisringe berechnen

A_gesamt = pi * (20^2 - 4^2) = 384·pi

A_20cm = pi * (10^2 - 4^2) = 84·pi

D.h. auf der 20 cm Rolle befinden sich noch etwa 10000/384*84 = 2187 Etiketten

A_10cm = pi * (5^2 - 4^2) = 9·pi

D.h. auf der 10 cm Rolle befinden sich noch etwa 10000/384*9 = 234 Etiketten

Comments

DANKE FÜR SCHNELLE ANTWORT!!!

könnte ich bitte die genauen schritte der rechnung haben???

komme mit dem klammerrechnen nicht so klar

nochmal allerhezlichsten dank

---

Hm. Weißt du jetzt nicht wie du (20² - 4²) berechnen sollst?

Im zweifel 20*20 - 4*4 = 384

Wenn du das pi weglässt, dann brauchst du da auch keine klammern setzen. Das pi ist hier eigentlich auch nicht notwendig, da dieses durch den quotienten eh gekürzt werden kann.

---

hallo

folgende Überlegung

wenn auf der vollen rolle 10.000 Etiketten sind

dann sind auf der halben rolle zwar keine 5000 Etiketten .....

aber  2187 kommt mir etwas arg wenig vor???!!!

gruß bernd

---

Stell dir das einfach vor wie eine Rolle Tesafilm. Dann hast du einen ganz langen Tesastreifen auf der Rolle.

________________________________________________________________________________

Von der Seite gesehen ist dieser Streifen ein Rechteck. Und die Rechtecksfläche ist proportional zur Streifenlänge.

Kannst du so weit folgen?

Nun befindet sich der Streifen aufgerollt auf einer Rolle. Dort bildet jetzt der Kreisring die Fläche des Tesastreifens. D.h. die Länge des Tesasreifens ist proportional zur Kreisfläche, die der Streifen bildet.

Schau dir das mal von der Seite an: Die Ringflächen sind hier die aufgerollten Streifen.

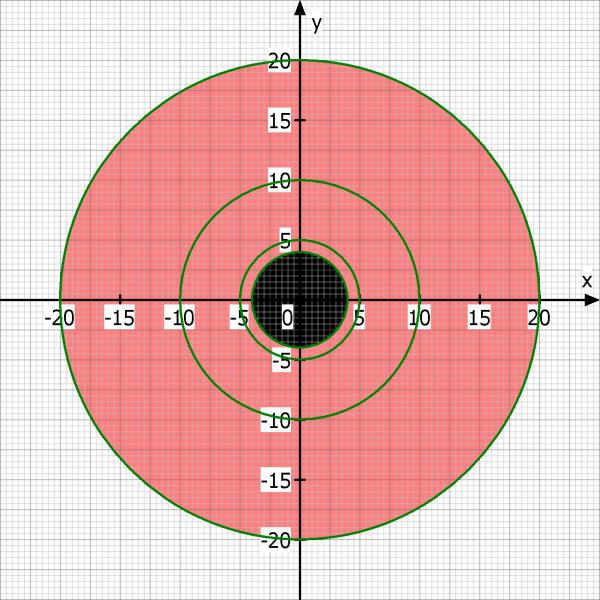
Bei der halbvollen Rolle fehlt also der äußere Ring. Stell dir das mal vor. Denkst du das immer noch das 2187 Etiketten zu wenig sind?