Hallo Luka,
beides gleich zu setzen wäre eine Möglichkeit. Aber da ist noch der Parameter \(a\). Und ich nehme mal an, dass die Frage ist: welchen Wert muss \(a\) haben, damit die Gerade parallel zur Ebene verläuft?
Damit dies der Fall ist, muss der Richtungsvektor der Geraden, von den beiden Richtungsvektoren der Ebene linear abhängig sein. Das bedeutet, dass sich der eine über eine Linearkombination der beiden anderen ausdrücken lässt - heißt formal - es muss gelten:
$$\begin{pmatrix}2 \\ -1\\ 5\end{pmatrix} \cdot r + \begin{pmatrix} 1\\ 3\\ -2\end{pmatrix} \cdot s = \begin{pmatrix} 3\\ 2\\a \end{pmatrix}$$
Dazu löst man zunächst das Gleichungssystem aus den oberen beiden Zeilen
$$\begin{pmatrix} 2 & 1\\ -1 & 3\end{pmatrix} \cdot \begin{pmatrix} r\\ s\end{pmatrix}= \begin{pmatrix} 3\\ 2\end{pmatrix}$$
das macht \(r=1\) und \(s=1\) und setzt das in die dritte Gleichung ein. Man erhält für \(a\):
$$5 \cdot 1 +(-2) \cdot 1 = a = 3$$
Zum Schluss muss man noch prüfen. ob der Aufpunkt \((1|2|3)\) nicht(!) in der Ebene liegt. Sonst wäre die Gerade Teil der Ebene. Dazu setzt man den Aufpunkt mit der Ebene gleich.
$$\begin{pmatrix}3 \\ 1\\0 \end{pmatrix} + \begin{pmatrix}2 \\ -1\\ 5\end{pmatrix} \cdot r + \begin{pmatrix} 1\\ 3\\ -2\end{pmatrix} \cdot s = \begin{pmatrix}1 \\ 2\\3 \end{pmatrix}$$
Den konstanten Vektor auf die rechte Seite bringen und als Lineares Gleichungssystem (LGS) schreiben:
$$\begin{pmatrix}2 & 1 \\ -1 & 3\\ 5 & 3\end{pmatrix} \cdot \begin{pmatrix} r\\ s\end{pmatrix} = \begin{pmatrix}-2 \\ 1\\3 \end{pmatrix}$$
Dieses LGS ist überbestimmt, da für zwei Unbekannte drei Gleichungen gegeben sind. Aus den ersten beiden Gleichung würde folgen, dass \(r=-1\) und \(s=0\) ist. Das erfüllt aber die dritte Gleichung nicht. Es gibt keine Lösung - daraus folgt, dass der Aufpunkt nicht in der Ebene liegt. Die Gerade liegt mit \(a=3\) parallel zu der Ebene.
Ich habe Dir das ganze noch mal in Geoknecht-3D eingegeben
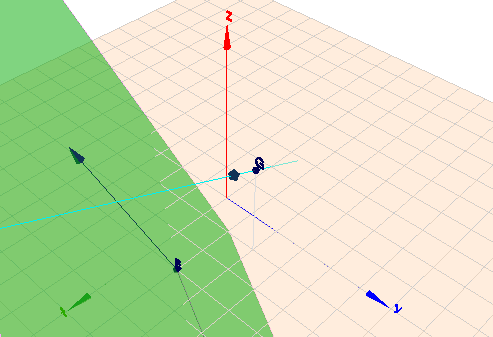
(klick auf das Bild)
Gruß Werner