Natürlichen Logarithmus ableiten. 6) f (x)=ln (x/(x+1)) (x im Zähler und x+1 im Nenner)

Question

Geben Sie zunächst die Definitionsmenge an und bestimmen Sie dann die 1. Ableitung. 

1) f (x)= ln (x-2)

2)f (x)=ln (5x)

3) f (x) = ln (-x) 

4) f (x) = ln (Wurzel x) 

5) f (x)= ln(1/x)

6) f (x)=ln (x/(x+1)) (x im Zähler und x+1 im Nenner) 

Meine Lösungen:

1) 1/(x-2) , x darf nicht 2oder kleiner sein sein

2) 1/x  , x darf nicht 0/negativ sein 

3) 1/x , x darf nicht /positiv0 sein 

4) 1/2x , x darf nich 0 oder negativ  sein 

5) -(1/x) , x darf nicht 0 oder kleiner sein

6) Hier hadert es bei mir, da ich nicht auf ein Ergebnis komme. Ich würde mir hier eine Lösung mit ausfühlichem Rechenweg freuen. Ebenfalls sollen wir hier keine Quotientenregel anwenden, sondern umformen und Produktregel und kettenregel benutzen. 

Zudem bin ich mir nicht genau sicher was eine Definitionsmenge genau ist und wäre dankbar, wenn mir das jemand erlöutern könnte. 

M.f.G

Answer 1

6) f (x)=ln (x/(x+1)) (x im Zähler und x+1 im Nenner) 

         =  ln ( (x+1) / (x+1)  -   1 / (x+1) ) 

     =    ln ( 1  -   1 / (x+1) ) 

f ' (x) =  1 /  (   1 - 1/ (x+1) )  *   ( 0 -    -1 / (x+1)²  )

=  (x+1) / x        *  1 / (x+1)²  

= 1 / ( x *(x+1)) 

Answer 2

1) f (x)= ln (x-2) 

2)f (x)=ln (5x) 

3) f (x) = ln (-x)  

4) f (x) = ln (Wurzel x)  

5) f (x)= ln(1/x) 

6) f (x)=ln (x/(x+1)) (x im Zähler und x+1 im Nenner) 

Meine Lösungen:

1) 1/(x-2) , x darf nicht 2oder kleiner sein sein. gut.

2) 1/x  , x darf nicht 0/negativ sein . gut.

3) 1/x , x darf nicht 0/positiv sein . ja.

4) 1/2x , x darf nicht 0 oder negativ  sein.  1/2x . Bitte eindeutiger schreiben. Klammer vergessen? Rechenweg?

5) -(1/x) , x darf nicht 0 oder kleiner sein. richtig. 

Du kannst übrigens alle deine Ableitungen bei "Derivative" kontrollieren. 

Bsp. https://www.wolframalpha.com/input/?i=ln+(√(x)) hat bei 4) 1/(2x) 

6) Hier hadert es bei mir, da ich nicht auf ein Ergebnis komme. Ich würde mir hier eine Lösung mit ausfühlichem Rechenweg freuen. Ebenfalls sollen wir hier keine Quotientenregel anwenden, sondern umformen und Produktregel und kettenregel benutzen. 

Zudem bin ich mir nicht genau sicher was eine Definitionsmenge genau ist und wäre dankbar, wenn mir das jemand erlöutern könnte. 

Hier kannst du auch mal bei Wolframalpha schauen, was herauskommen könnte:

https://www.wolframalpha.com/input/?i=ln+(x%2F(x%2B1)) 

Nach Logarithmengesetzen kannst du auch schreiben:

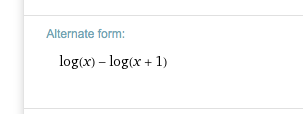
für  x > 0 (wenn du in den Zwischenresultaten reell bleiben möchtest). 

f'(x) = 1/x - 1/(x+1) = ((x+1) - x)/(x(x+1)) = 1/(x(x+1)) 

Möglich ist aber auch der Fall x<-1. 

Hier dann die gleiche Ableitung wie oben ( Die ganzen Minus sollten wieder verschwinden)