Teilmenge bestimmen, sodass die Funktion umkehrbar ist

Question

Hallo an Alle,

Die Teilmengen M1 und M2 sollen so bestimmt werden, dass die Funktion pi : Di →Bi : x →p(x) 

für i=1,2 umkehrbar ist. Die Funktion lautet: p (x) = 2x2 −x+3.

Wie bestimme ich diese Teilmenge?

Wie viele Lösungen x ∈ Di besitzt die Gleichung y=p(x) nun für y ∈ Bi ?

Comments

Vom Duplikat:

Titel: Teilmenge bestimmen, sodass die Funktion umkehrbar ist?

Stichworte: funktion,umkehrbar,mehrdimensional,menge,mengenlehre

Hallo an Alle,

Die Teilmengen M1 und M2 sollen so bestimmt werden, dass die Funktion pi : Di →Bi : x →p(x) 

für i=1,2 umkehrbar ist. Die Funktion lautet: p (x) = 2x2 −x+3.

Wie bestimme ich diese Teilmenge?

Wie viele Lösungen x ∈ Di besitzt die Gleichung y=p(x) nun für y ∈ Bi ?

Answer 1

Hallo Chanelle,

bei den beiden Funktionen  p_i : D_i →B_i : x  ↦  p_i(x) =  2x² −x + 3 handelt es sich um zwei  Teilparabeln mit gleicher Vorschrift  und verschiedener Definitionsmenge, weil diese Funktionen nur dann umkehrbar sind, wenn sie über ihrem Definitionsbereich D_i  streng monoton sind. 

Mit der Scheitelform  y = a · (x - x_s)² + y_s   erhält man 

M₁ = D₁ =  ] - ∞ ; x_s ]   und  M₂ = D₂ = [ x_s ; ∞ [         (maximale Teilmengen von ℝ)

       ( B_i = [ y_s ; ∞ [   ist die Bildmenge beider Funktionen ) 

 p_i(x)  =  2x² −x + 3  =  2 · [ x - 1/2 ·x ]  + 3  =   2 · [ x - 1/2 ·x  + (1/4)² - 1/16 ]  + 3

          =  2 · [ (x - 1/4)² - 1/16 ]  + 3  =  2·(x - 1/4)² - 1/8  + 3

p_i(x)  =   2·(x - 1/4)² + 23/8             Scheitelpunkt: ( 1/4 | 23/8 )

p₁ :    ] - ∞ ; 1/4 ]  →  [ 23/8 ; ∞ [   ;  p₁(x)  =   2·(x - 1/4)² + 23/8  

p₂ :    [ 1/4 ; ∞ [   →   [ 23/8 ; ∞ [   ;  p₂(x)  =   2·(x - 1/4)² + 23/8  

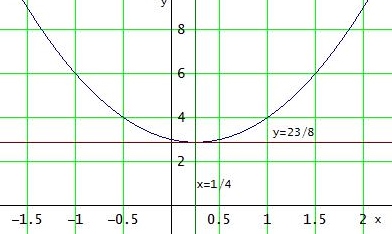
> Wie viele Lösungen x ∈ Di besitzt die Gleichung y=p(x) nun für y ∈ Bi ?

Über diesen Definitionbereichen haben die Gleichungen genau eine Lösung.

Gruß Wolfgang

Answer 2

Vermutlich sind die M_i ja die D_i und B_i .

Das ist eine quadratische Funktion, der Graph also eine

Parabel. Scheitelpunkt erkennst du nach

Umformung auf p(x) = 2* ( x-1/4)² + 5/2 als  S( 1/4  ;  5/2 )

Also 1. Lösung  D1 = ] - ∞ ; 1/4 ]  und  B1 = [ 5/2 ;  ∞ [

oder eben  D2 = [ 1/4 ;   ∞ [  und  B2 = [ 5/2 ;  ∞ [