man sollte sich vor dem Lösen mit Hilfe eines Zeit-Weg-Diagramms klar machen, wann welcher Zug wo ist. Das könnte so aussehen:
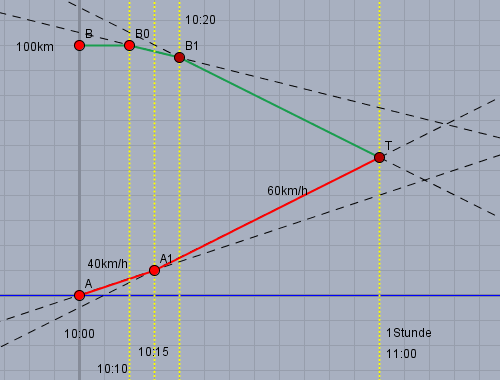
nach rechts geht die Zeitachse und nach oben die Weg-Achse. Der Zug \(A\) ist um 10:00 bei der Position 0km. Der Zug \(B\) ist 100km entfernt - also bei Position 100km. Jede Bewegung mit konstanter Geschwindigkeit zeichnet sich in dem Diagramm als Gerade. Zug \(A\) fährt mit 40km/h los. Seine Weg-Funktion ist zu diesem Zeitpunkt
$$s_A(t) = 40\frac{\text{km}}{\text{h}} \cdot t$$
\(t\) ist die Zeit. D.h. wenn der Zug \(A\) so weiter fahren würde, wäre er nach einer Stunde bei Position \(40\text{km/h} \cdot 1\text{h}=40\text{km}\). Und nach 15min d.h 1/4Stunde ist er bei
$$s_A(t=\frac14 \text{h}) = 40\frac{\text{km}}{\text{h}} \cdot \frac14 \text{h} = 10 \text{km}$$
Das ist die Position \(A_1 = (10:15; \space 10\text{km})\) in dem Diagramm. Von dort geht es mit 60km/h weiter - dann wird seine Weg-Funktion (rot) zu
$$s_A(t)= 10 \text{km} + 60\frac{\text{km}}{\text{h}} \cdot (t - 15\text{min})$$
Genauso geht man bei \(B\) vor. Dieser Zug startet aber erst um 10:10 und seine Geschwindigkeit ist 'negativ', da er in dem gewählten Koordinatensystem in Richtung kleinerer Positionen fährt. Seine Weg-Funktion (grün) ist zunächst:
$$s_B(t) = -30 \frac{\text{km}}{\text{h}}(t - 10\text{min}) + 100 \text{km}$$
Diese Funktion gilt natürlich erst ab \(t \ge 10\text{min}\). Nach 10 weiteren Minuten (also bei \(t=20\text{min}\)) ist \(B\) bei
$$s_B(t=20\text{min}) = -30 \frac{\text{km}}{\text{h}}(20\text{min} - 10\text{min}) + 100 \text{km}$$
$$\space = -30 \frac{\text{km}}{\text{h}}(\frac16 \text{h}) + 100 \text{km} = 95\text{km}$$
Dies ist die Position \(B_1\). von dort geht es weiter mit -60km/h:
$$s_B(t)= 95\text{km} - 60 \frac{\text{km}}{\text{h}} \cdot (t - 20\text{min})$$
Auf dem folgenden Wegstück treffen sich beide Züge. Dies ist genau dann der Fall, wenn
$$s_A(t)=s_B(t)$$
das setze ich jetzt ein:
$$10 \text{km} + 60\frac{\text{km}}{\text{h}} \cdot (t - 15\text{min})=95\text{km} - 60 \frac{\text{km}}{\text{h}} \cdot (t - 20\text{min})$$
und erhalte \(t=1h\) und die Position ist \(55\text{km}\). Falls Du Fragen hast, so melde Dich bitte.
Gruß Werner